Viele in der Natur vorkommende Objekte können mathematisch durch dreidimensionale Flächen beschrieben werden. Diese können durch Dreiecksnetze approximiert werden, weisen in der Regel jedoch eine komplexe topologische Struktur mit mehreren Löchern auf. Die meisten geometrischen Algorithmen können hingegen nur auf Flächen angewandt werden, die einer topologischen Scheibe entsprechen. Betrachtet man z.B. eine quadratische Fläche und verklebt gegenüberliegende Seiten, so entsteht daraus ein Torus, d.h. umgekehrt kann man den Torus als dreidimensionale Fläche in geschickter Weise aufschneiden und erhält eine zusammenhängende, scheibenförmige Fläche. In dieser Arbeit wird diese Idee aufgegriffen und verallgemeinert indem verschiedene Schnitte für beliebige andere Flächen mit mehr als nur einem Loch berechnet und verglichen werden, um daraus eine scheibenförmige Fläche zu erhalten.

Es werden zunächst eine Methode, sowie zwei Spezialisierungen davon erklärt, um einen initialen Schnitt einer gegebenen Fläche in Form eines Dreiecksnetzes zu berechnen. Danach werden Techniken gezeigt, wie man einen gegebenen Schnitt verbessern kann, hinsichtlich Länge und Lage der Schnittpfade. Zum Schluss wird noch eine weitere Möglichkeit einen Schnitt zu berechnen betrachtet, indem zuerst für jedes Loch der Fläche ein sog. Handle-Loop bestimmt wird.

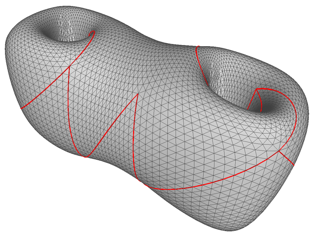Ein initialer Schnitt eines Doppeltorus

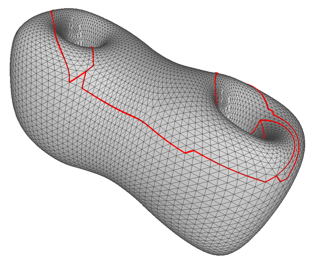Der initiale Schnitt von links verbessert, indem die Schnittpfade gekürzt wurden

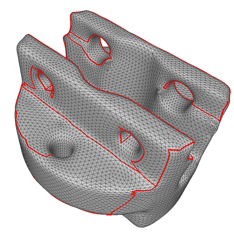Ein Schnitt entlang möglichst scharfer Kanten der Fläche

Eine wichtige Anwendung der in dieser Arbeit erklärten Verfahren, ist die Parametrisierung von Flächen. Die meisten der bekannten Parametrisierungsmethoden basieren nur auf topologisch scheibenförmigen Flächen. Um diese jedoch auch auf andere Flächen anzuwenden, findet man einen Schnitt der Fläche und bildet dann diesen passend ab auf den Parameterbereich. Eng mit der Parametrisierung von Flächen verbunden ist das Abbilden von Texturen auf eine Fläche. In dieser Anwendung sollen bestimmte Muster, die in der Regel als zweidimensionales Bild vorliegen, auf die Fläche durch eine stetige Funktion abgebildet werden. Um so etwas zu realisieren wird die Fläche aufgeschnitten und dann darauf die Textur gelegt und der Schnitt anschließend wieder rückgängig gemacht. Dabei kann es beim Wiederzusammenkleben der Fläche zu Ungenauigkeiten an den Klebestellen kommen, die dann an der Textur erkennbar sind. In dieser Arbeit wird der berechnete Schnitt so optimiert, dass solche Fehler weitestgehend vermieden werden.