Übersicht
In der Computergrafik sind dreidimensionale Netze für die Visualisierung nicht mehr wegzudenken. Oft müssen diese vereinfacht werden, um akzeptable Geschwindigkeiten für die Darstellung zu realisieren. Bei der Vereinfachung dieser Netze stellt der Hausdorff-Abstand ein wichtiges Gütemaß zum Vergleichen zweier Netze dar. Bisherige Verfahren bestimmten den Hausdorff-Abstand nur approximativ, indem Punkte über den Netzen verteilt und deren Abstand berechnet wurde.
Die Diplomarbeit realisiert eine neues Verfahren zur exakten Berechnung des Hausdorff-Abstands. Hierfür werden die Abstandsfunktionen zwischen Dreiecken explizit berechnet und über diesen das Maximum gesucht. Um die Parametergebiete der Abstandsfunktionen korrekt zu bestimmen mussten Anordnungen von Kegelschnitten in der Ebene betrachtet werden. Diese sind speziell bei dem hier angewendeten Verfahren numerisch instabil zu berechnen. Deswegen wurde zwei Lösungsansätze verfolgt. Der erste Ansatz berechnet die Anordnungen mit Hilfe exakter Arithmetik. Der zweite Ansatz berechnet die Anordnungen mittels Gleitkomma-Arithmetik und verwendet, um eine korrekte topologische Anordnung zu gewährleisten, spezielle Prädikate, die effizient auszuwerten sind, jedoch immer ein korrektes Ergebnis liefern. Um möglichst wenige Dreiecke für den Abstand betrachten zu müssen wurde ein Raumunterteilungsverfahren implementiert, dass es ermöglicht, den Abstand nur zu nahen Dreiecken berechnen zu müssen. Zusätzlich wurde eine Abschätzung des Hausdorff-Abstands angegeben, die es ermöglicht vorherzusagen, welche Dreiecke betrachtet werden müssen.
Um die Ergebnisse überprüfen und mit anderen Verfahren vergleichen zu können wurde zusätzlich zur Abstandsberechnung die Visualisierung der quadratischen Abstandsfunktionen realisiert, die in echtzeit betrachtet werden können. Hierfür wurde eine Delaunay-Triangulierung über den Anordnungen berechnet und die quadrierten Abstandsfunktionen ausgewertet. Die Abstandsfunktionen können dann mit Hilfe ihres Wertes farblich kodiert werden.
Ergebnisse
Das implementierte Verfahren wurden anhand mehrere Beispiel getestet. Der Abstand zu nicht zusammenhängenden Netzen kann sowohl mit exakter als auch mit inexakter Arithmetik schnell berechnet werden. Dies liegt daran, dass die numerischen Probleme vorallem bei zusammenhängenden Netzen auftreten, was die Laufzeiten mit exakter Arithmetik ansteigen lässt. Mit inexakter Arithmetik sind die Laufzeiten bei zusammenhängenden Netzten deutlich besser als mit exakter Arithmetik, es kann hier jedoch noch zu Fehlern kommen. Den Abstand zwischen zwei unterschiedlich fein aufgelösten Köpfen des Stanford-Bunnys zu berechnen betrug z. B. mit exakter Arithmetik etwas mehr als zwei Stunden.
 |
 |
 |
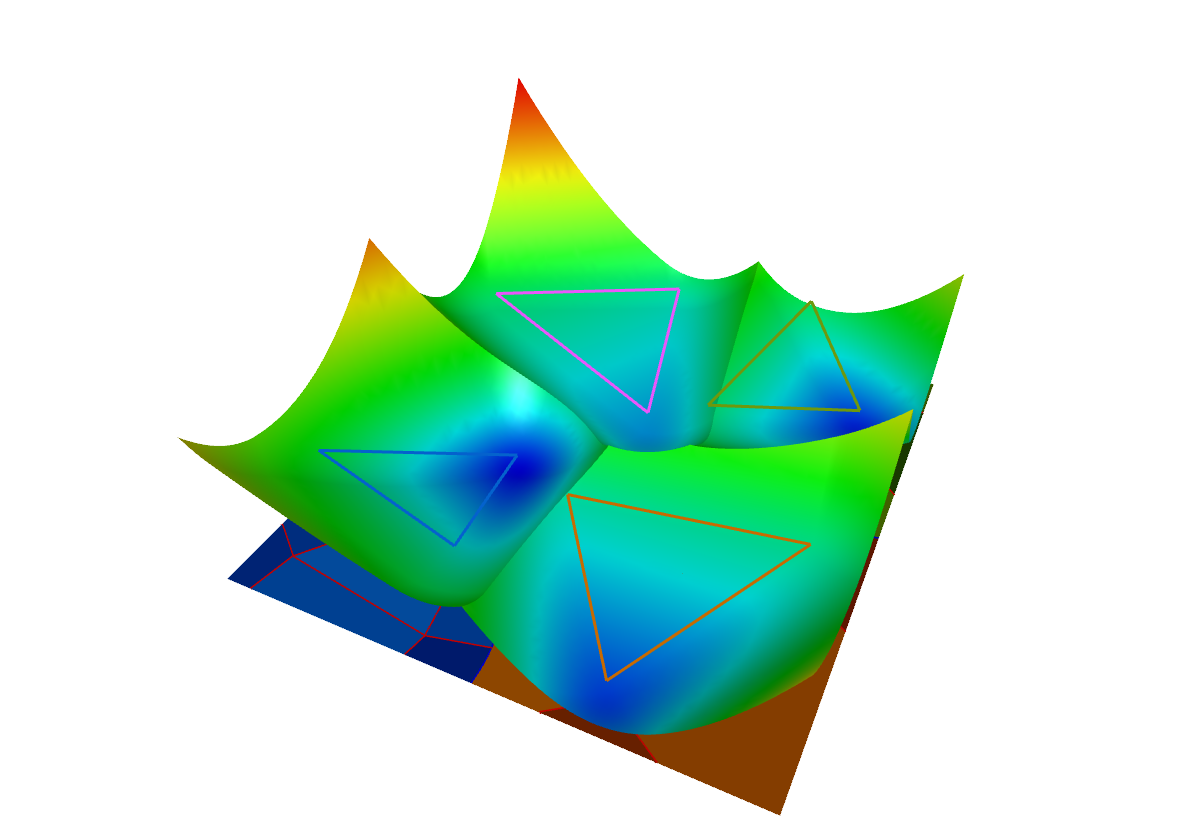 |
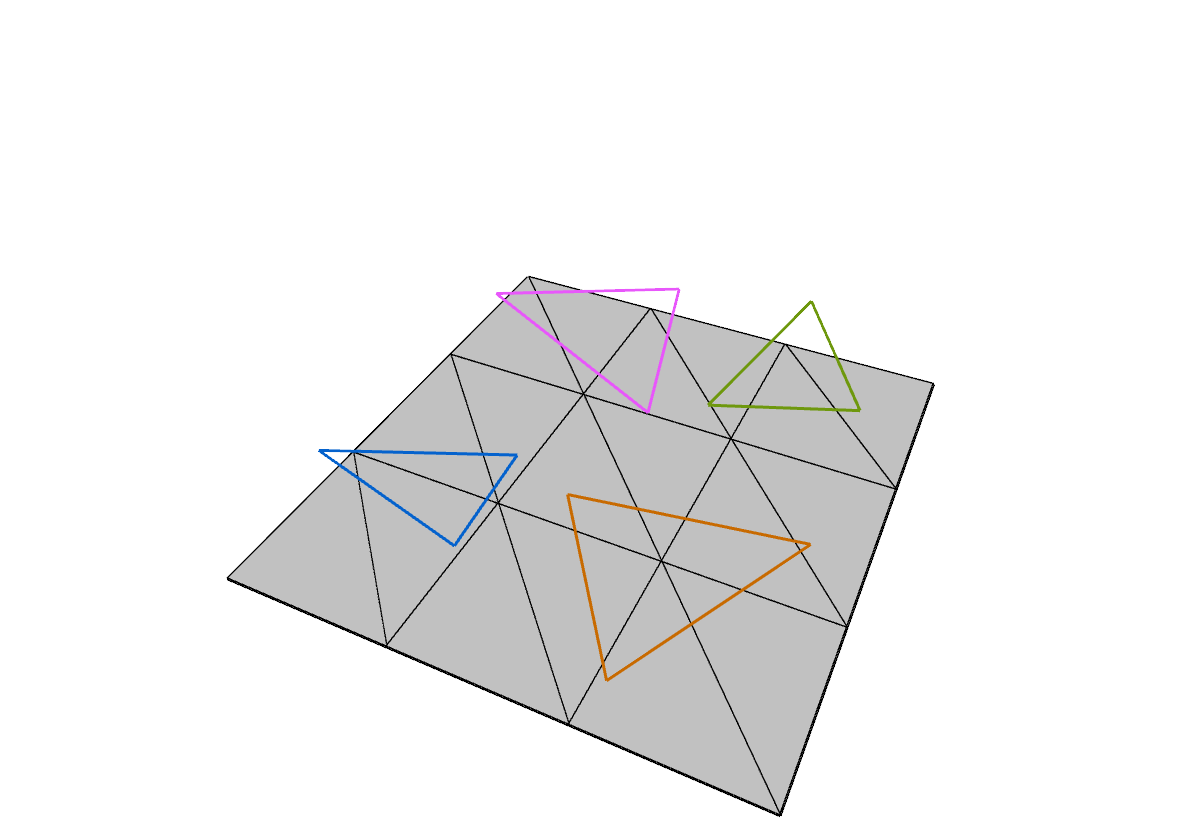
| Abstandsberechnung eines Quadrats zu nicht zusammenhängenden Dreiecken:
Der Abstand der 18 grauen Dreiecke wurde zu vier zufällig gewählten Dreiecken bestimmt (oben links). Hierfür wurden die Anordnungen der einzelnen Parametergebiete (oben rechts) der quadratischen Abstandsfunktionen berechnet (unten links). Die Abstandsfunktion kann auch farblich kodiert dargestellt werden (unten rechts). |
|
 |
 |
 |
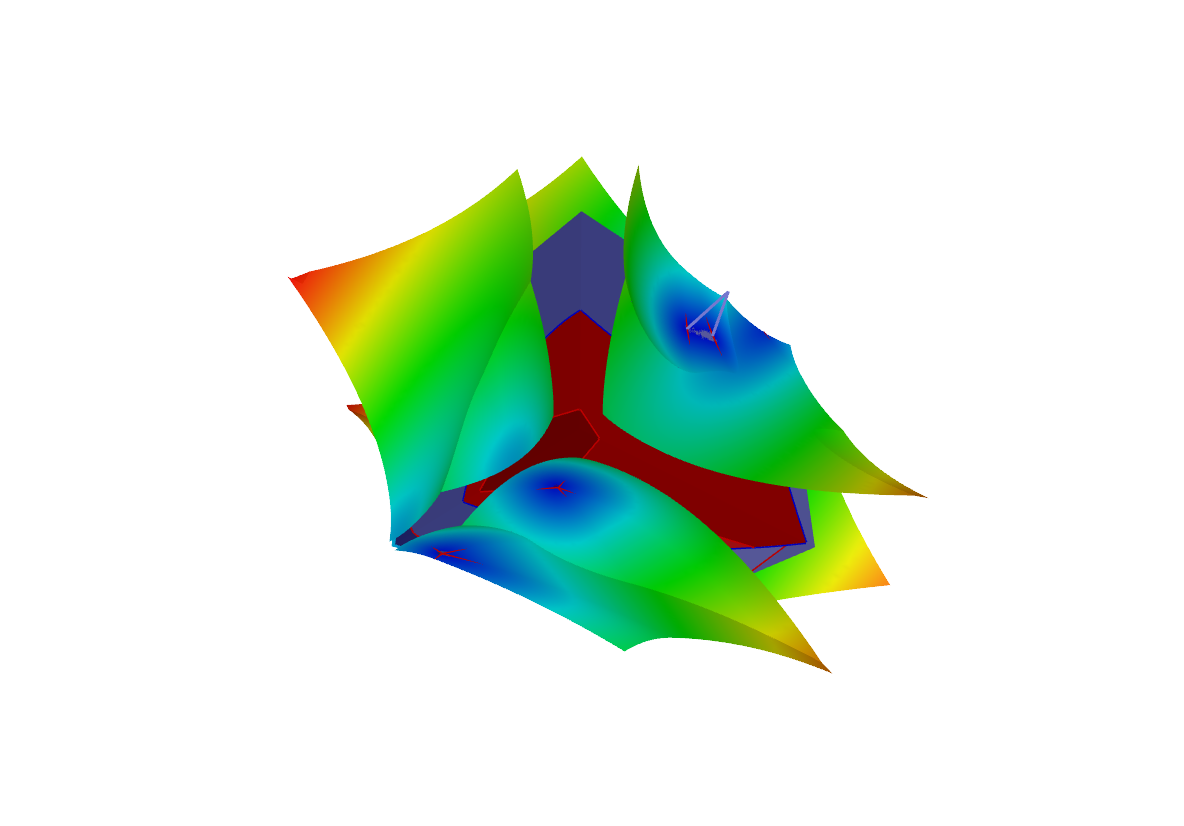 |
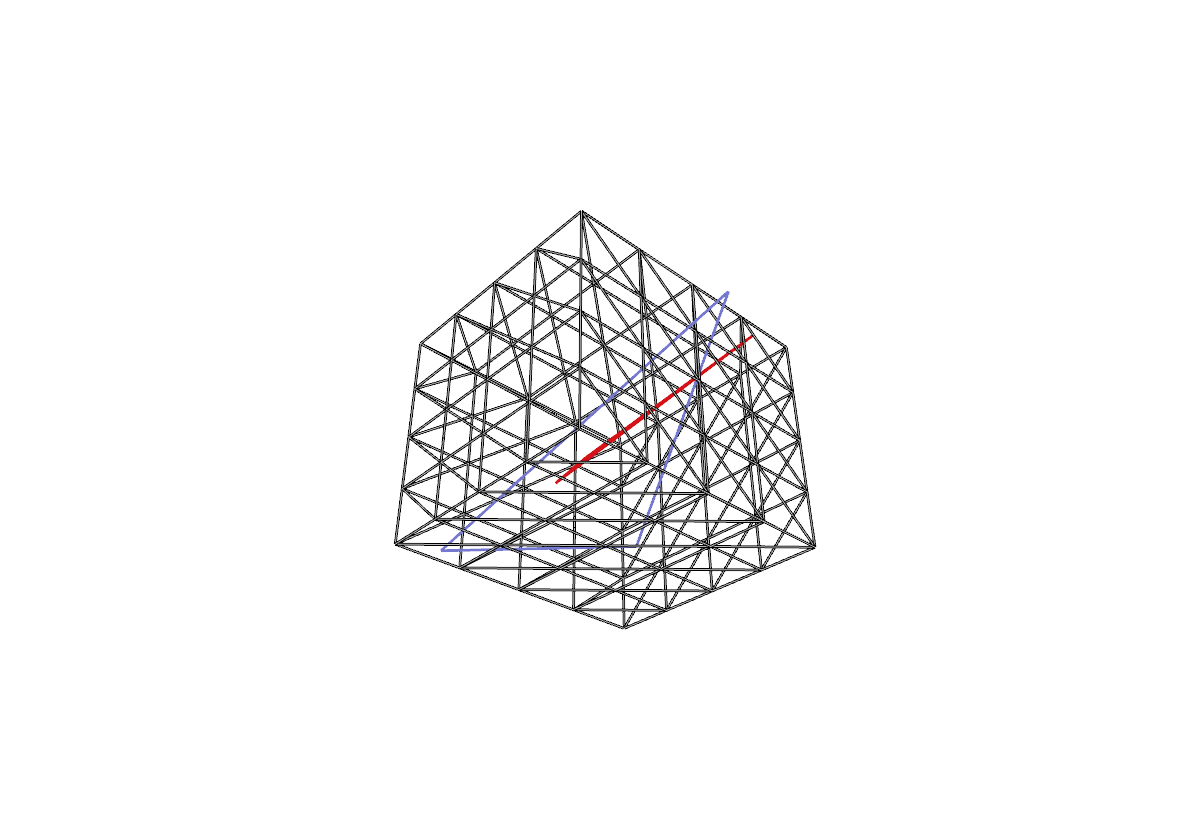
| Abstandsberechnung zwischen einem Würfel und zwei im Inneren liegenden Dreiecken (oben links) mit den Anordungen für die Parametergebiete (oben rechts) der quadrierten Abstandsfunktionen (unten links). Der Abstands kann zusätzlich farblich kodiert werden (unten rechts). |
|

|
 |
 |
 |
 |
 |
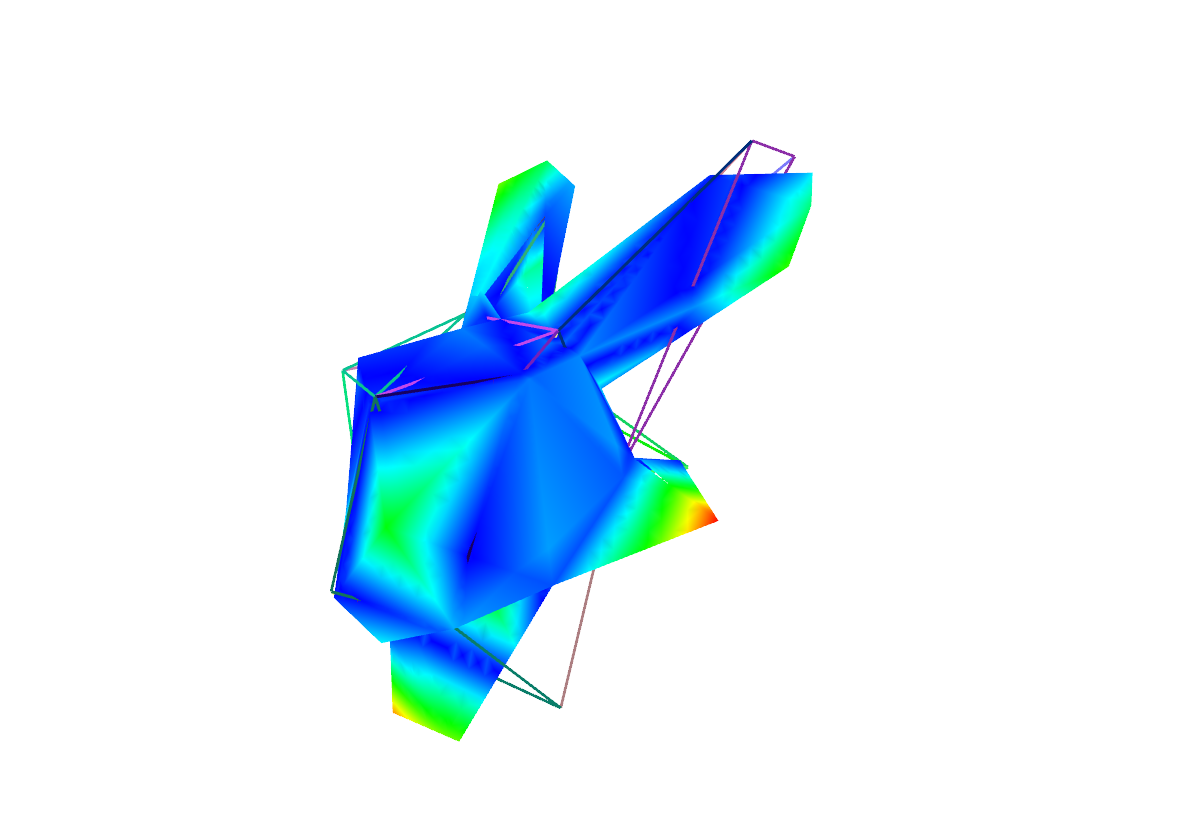 |
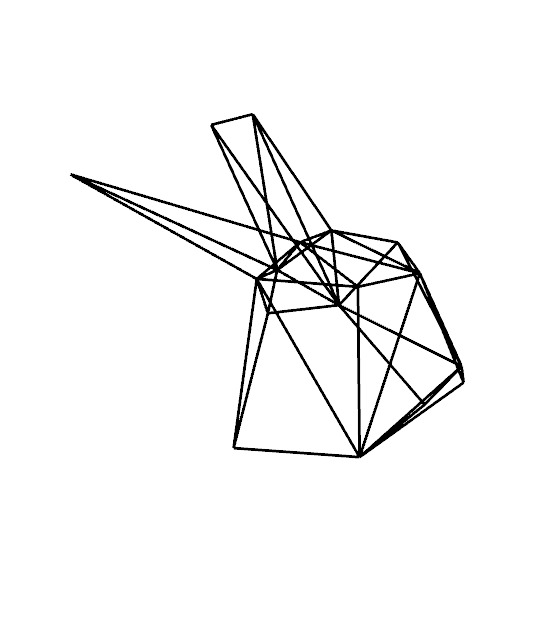
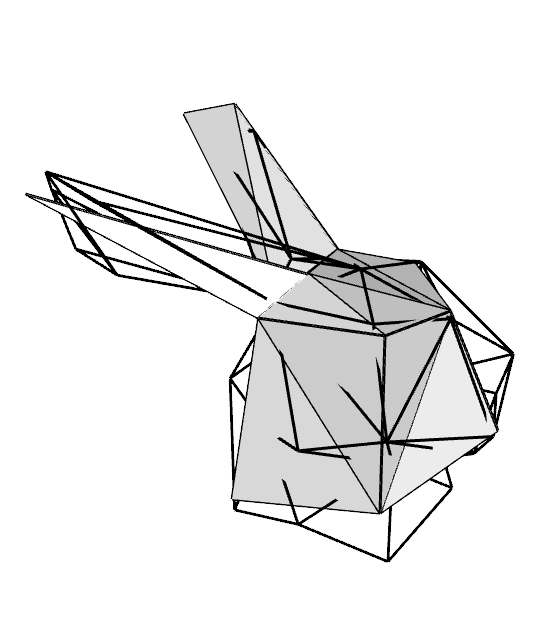
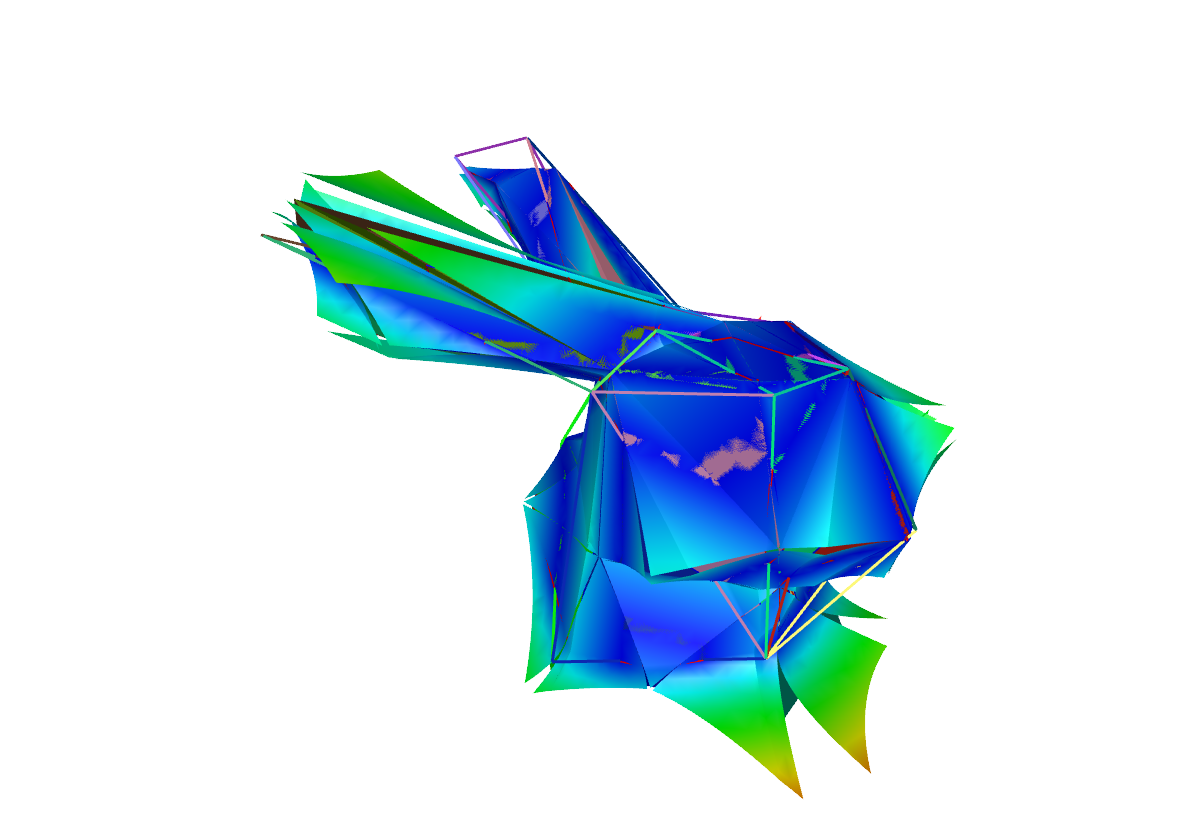
| Abstandsberechnung zwischen einem fein aufgelösten (oben links) und einem grob aufgelösten Modell (oben mitte) des Stanford Bunnys mit den berechneten Anordnungen (mitte links) und den dazugehörigen quadratischen Abstandsfunktionen (mitte rechts). Das Modell kann auch direkt mit den farblich kodierten Abstand angezeigt werden (unten links und unten rechts). |
|
Ausblick
Insgesamt ergaben die Vergleiche mit approximativen Verfahren keine großen Abweichungen zur exakten Bestimmung des Hausdorff-Abstands. Die langen Laufzeiten mit exakter Arithmetik und die numerischen Probleme mit inexakter Arithmetik zeigen aber deutlich, dass für die meisten Anwendungen die approximativen Verfahren vorzuziehen sind. Vorteil der exakten Methode könnte es jedoch sein, den mittleren Hausdorff-Abstand zu berechnen, indem das Integral über den quadrierten Abstandsfunktionen betrachtet wird.
