Übersicht
Im Laufe der letzten Jahre und Jahrzehnte bildeten sich im Zuge der Erforschung mathematischer Freiformdarstellungen in der Computergrafik einige Methoden heraus, die gewisse theoretische Stetigkeitsvorgaben erfüllen. Meist begnüte man sich jedoch mit dem Existenzbeweis oder dem Beweis der Stetigkeit des entsprechenden Verfahrens. Wie schnell klar wurde, unterscheiden sich diese jedoch weniger in den theoretischen als den praktischen Eigenschaften wie der Krümmungsverteilung oder den Isophoten. In dieser Diplomarbeit werden aktuelle Verfahren zur Erzeugung von C1- und C2-stetigen Flächen vergleichend analysiert und anhand ihrer Qualität in Beziehung gesetzt.
Details
Kontrollnetze von Freiformflächen beliebiger Topologie weisen stets sogenannte Ausnahmepunkte auf. Dies sind, beispielsweise in einem Vierecksnetz, Knoten, an denen n ≠ 4 Vierecke zusammenlaufen. Man kann zeigen, dass die Ableitungsbedingungen an derartigen Punkten einem zyklischen System genügen müssen, und es deshalb nur über Umwege möglich ist, höhere Stetigkeitsanfordeungen zu formulieren.
Seit den einschlägigen Veröffentlichungen zu Unterteilungsalgorithmen im Jahre 1978 kennt man einfache Methoden, wie man auch in solchen Situationen durch wiederholte Anwendung von Knoten- und Kanteneinfügeregeln eine glatte, das heißt C1-stetige, Limesfläche erzeugen kann. Die so gewonnenen Flächen besitzen jedoch eine Reihe von Unzulänglichkeiten, unter denen die divergenten Hauptkrümmungen am Ausnahmepunkt die prominenteste ist.
Neben den Unterteilungsalgorithmen gibt es einige weitere Ansätze, die sogar C2-Stetigkeit an Ausnahmepunkten ermöglichen. Dazu zählen unter anderem die 1997 veröffentlichten Freiformsplines. Dort wird die Umgebung eines infragekommenden Ausnahmepunktes als n-seitiges Loch angesehen, das mit Hilfe einer passend erzeugten quadratischen Fläche gefüllt wird.
Darauf aufbauend wurde 2005 die sogenannte Guided Subdivision vorgestellt, die die Probleme der Freiformsplines auf elegante Art und Weise behebt und dadurch große Flächengüte und Flexibilität erlaubt. Um von der starren Füllfläche der Freiformsplines zu abstrahieren, wird nun eine beliebig gegebene Fläche verwendet und in Schablonenform abgetastet, die den üblichen Unterteilungsmustern ähnelt.
Ein weiteres Verfahren ist das 2006 präsentierte Flächenmischen. Hier macht man sich zunächst auch einen Unterteilungsalgorithmus zunutze, indem man ihn etwa zwei Mal anwendet und die dadurch erhaltenen Kontrollpunkte als Grundlage für eine approximativ erzeugte Paßfläche verwendet. Mittels einer geeignet definierten Gewichtsfunktion oder über Energiemaße erreicht man C2-Stetigkeit (im Sinne differenzierbarer Mannigfaltigkeiten).
Die vierte untersuchte Methode basiert auf der ebenfalls schon länger bekannten Idee der Energieminimierung diskreter Flächen. 2007 wurde ein Minimal-Mittlerer-Krümmungsfluß sechster Ordnung, MMCVF genannt, beschrieben, der nach Behauptung der Autoren G2-Stetigkeit erreicht. In einer Testimplementierung wurden die wesentlichen Schritte des Algorithmus nachvollzogen, die sich unter anderem aus der Diskretisierung differentialgeometrischer Maße und im Aufstellung und Lösen eines dünn besetzten Gleichungssystems zusammensetzen.
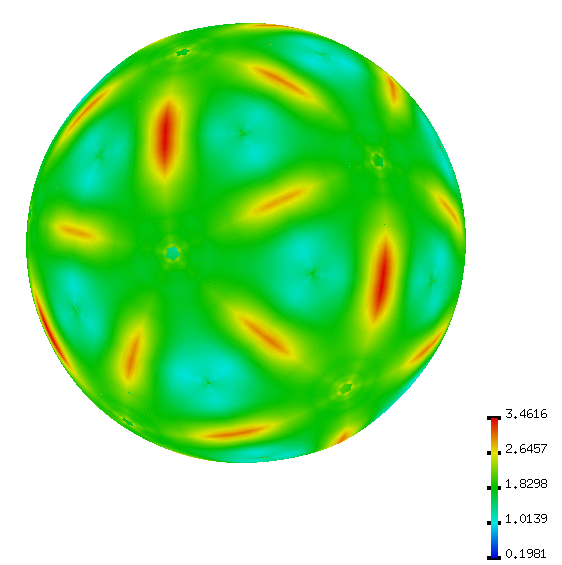 |
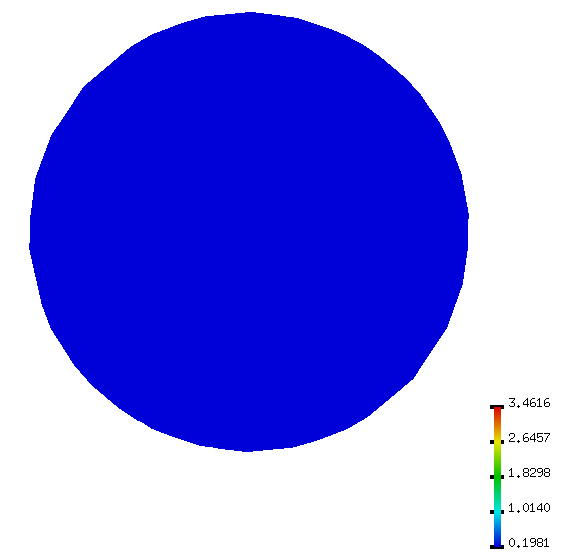 |
| (links) Mittlere Krümmung einer Catmull-Clark-Fläche nach viermaliger Anwendung auf einen Dodekaeder. Man erkennt die unregelmäßige Krümmungsverteilung anhand der verschiedenen Farben. (rechts) MMCVF-Anwendung auf dasselbe Anfangsnetz. Die mittlere Krümmung ist wie bei einer Sphäre zu erwarten überall gleich. | |
Die folgende Abbildung zeigt die Gaußkrümmung für alle untersuchten Verfahren.
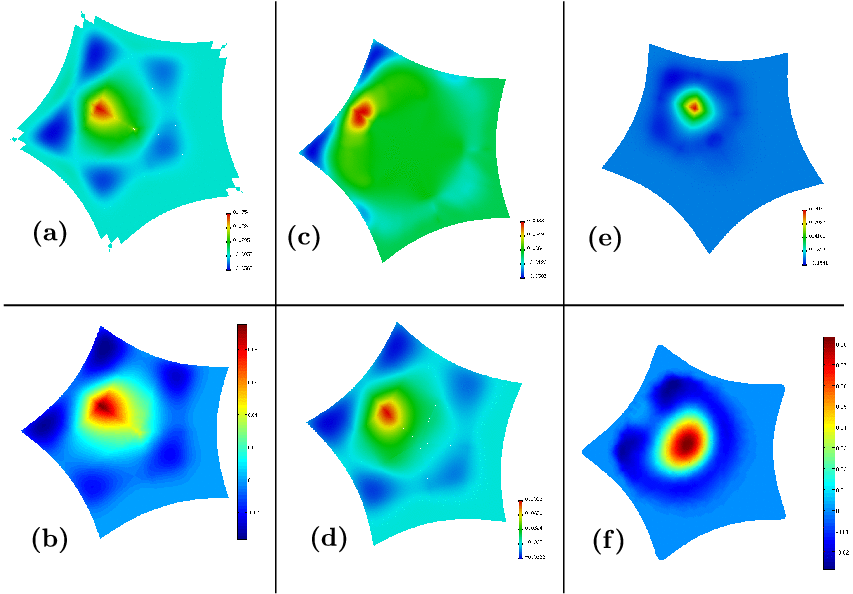 |
| (a) Catmull-Clark-Unterteilungsalgorithmus, (b) Flächenmischen, (c) Freiformsplines mit Grad (6,6), (d) Freiformsplines mit Grad (13,13), (e) Guided Subdivision, (f) MMCVF |
Ein weiterer Gradmesser der Flächengüte sind die sogenannten Highlightlinien, deren Vergleichsbilder in der nächsten Abbildung zu sehen sind.
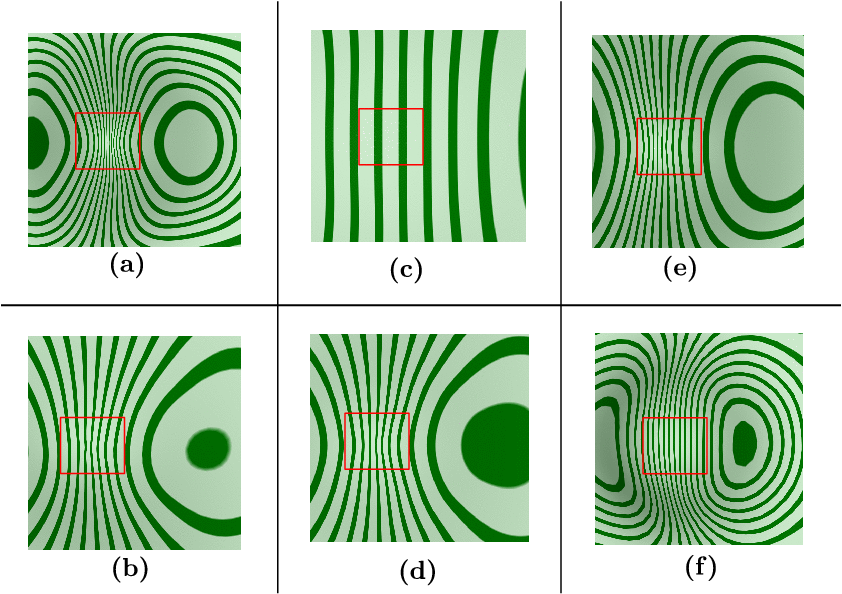 |
| (a) Catmull-Clark-Unterteilungsalgorithmus, (b) Flächenmischen, (c) Freiformsplines mit Grad (6,6), (d) Freiformsplines mit Grad (13,13), (e) Guided Subdivision, (f) MMCVF |
Ergebnisse
Es wurde deutlich, dass alle Verfahren in der Lage sind, die Umgebung um Ausnahmepunkte auf ansehnliche Weise zu füllen. Bei Ausnahmepunkten niedrigerer Valenz liegen die Freiformflächen qualitativ gleichauf mit der Guided Subdivision. Erst ab n ≥ 8 zeigen sich merkliche Vorteile für letztere. Um die Abbildungsfähigkeiten der Guided Subdivision hinsichtlich beliebiger Lenkflächen zu demonstrieren, wurde diese ebenfalls testweise unter Verwendung der Freiformsplines vom Grad (13,13) als Lenkfläche implementiert. Die Implementierung bestätigte die theoretischen Ergebnisse. Insgesamt liefert die Guided Subdivision die besten Ergebnisse. Schon öfter in der Literatur besprochenen Mischprobleme zeigten sich auch beim Flächenmischen, so dass die damit erzeugten Flächen zwar C2-stetig sind, aber dem Vergleich mit den anderen Verfahren nicht standhalten.
Trotz seiner rein diskreten Arbeitsweise wusste auch der MMCVF zu überzeugen. Als universelles Verfahren angelegt, konnte mit einer Implementierung gezeigt werden, dass sowohl die Konvergenz als auch die Limesflächen den formulierten Zielen genügen; Einschränkend muss allerdings gesagt werden, dass die Laufzeit des Algorithmus im Vergleich zu den anderen Verfahren sehr hoch ist.
