Das Thema dieser Studienarbeit ist die Berechnung minimaler Umkugeln. Eine minimale Umkugel ist die kleinste Kugel, die eine gegebene Punktwolke enthält. Solche Kugeln sind für zahlreiche Probleme aus verschiedenen Bereichen relevant, z.B. bei grafisch-geometrischen Algorithmen oder im Operations-Research. In dieser Studienarbeit werden drei verschiedene Algorithmen zur Berechnung von Umkugeln untersucht und ihre Vor- und Nachteile herausgestellt.

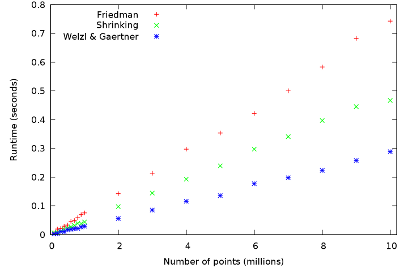
Auch wenn der bereits etablierte Algorithmus von Welzl & Gärtner bei den im Rahmen dieser Studienarbeit durchgeführten Laufzeittests am Besten abschneidet (Abb 1.), liegen seine Konkorrenten - der Algorithmus von Friedman und der Schrumpfalgorithmus - nicht weit hinter ihm und bestechen durch andere Vorteile. Diese sind z.B. die Online-Eigenschaft des Algorithmus von Friedman oder die Möglichkeit des Schrumpfalgorithmus, zu jedem Zeitpunkt (Rechenschritt) eine obere Schranke für die minimale Umkugel angeben zu können. Außerdem konnte gezeigt werden, dass der Algorithmus von Friedman im schlechtesten Fall mindestens quadratische Laufzeit benötigt (Abb. 2).

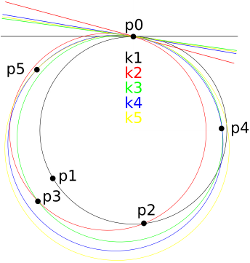Abbildung 1: Laufzeitvergleich der Algorithmen in der Ebene	Abbildung 2: Konstruktion eines Falles mit quadratischer Laufzeit für den Algorithmus  von Friedman

Nach dem Abschluss der Studienarbeit bleiben vor allem Fragen nach den asymptotischen Laufzeiten der untersuchten Algorithmen offen. Nur für den Algorithmus von Welzl & Gärtner gibt es aufgrund der bewiesenen erwarteten linearen Laufzeit eine einigermaßen befriedigende Antwort. Des Weiteren ist die Suche nach gut parallelisierbaren Algorithmen zur Berechnung minimaler Umkugeln ein Feld, das durch die aktuellen Entwicklungen in der Prozessortechnik an Bedeutung gewinnen dürfte.