Differentialgeometrische Konzepte für Dreiecksnetze
- Type:Diplomarbeit
- Date:2004
- Author(s):Martin Kilian
- Links:.PDF
.BIB -
Ziel dieser Arbeit war die strukturierte Darstellung der umfangreichen Literatur über diskrete differentialgeometrische Operatoren. Zentrale Begriffe in diesem Zusammenhang sind die diskrete Gaußkrümmung, das diskrete Normalenbild, die diskrete mittlere Krümmung und der diskrete mittlere Krümmungsvektor.
Für Anwendungen spielen der letztgenannte mittlere Krümmungsvektor [1] sowie die totale äußere Absolutkrümmung [2] eine wichtige Rolle. Alle aufgeführten Begriffe sind für orientierte polyedrische Flächen definiert und lassen sich unmittelbar für immersierte polyedrische Flächen, d.h. polyedrische Flächen mit globalen Selbstdurchdringungen, deuten. Die entsprechenden Sätze behalten dabei ihre Gültigkeit. Exemplarisch werden einige Begriffe und Resultate vorgestellt.
Die diskrete Gaußkrümmung
Die diskrete Gaußkrümmung in einer Ecke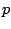 
einer polyedrischen Fläche ist die Differenz
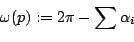
mit den an der Ecke anliegenden Winkeln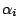 
. Diese Krümmung bleibt offenbar unter Isometrien, d.h. Verknickungen, der Fläche erhalten, was unmittelbar eine diskrete Version des theorema egregium liefert. Es ist anzunehmen, dass diese Tatsache bereits Gauß als Hinweis auf die Richtigkeit dieses berühmten Theorems deutete.
Diskretes Normalenbild und sphärische Indikatrix
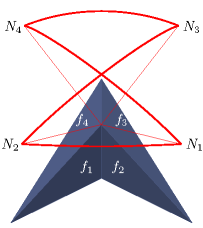
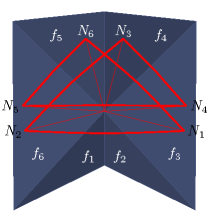
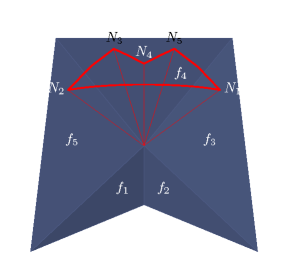
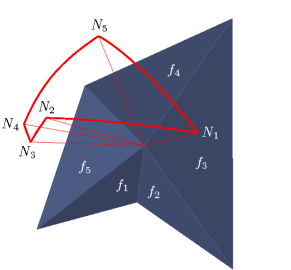
Die diskrete Gaußkrümmung lässt sich als orientierter Flächeninhalt des diskreten Normalenbildes interpretieren. Beispielhaft ist in den folgenden Abbildungen der Rand dieses Normalenbildes, die sogenannte sphärische Indikatrix, einiger Ecken polyedrischer Flächen zu sehen.
 |
 |
 |
 |
Als Approximation für die Gaußkrümmung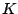 
einer regulären Fläche, der eine polyedrische Fläche einbeschrieben ist, bietet es sich nun folgendes an:
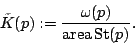
Unter Verwendung eines speziellen Abstandsbegriffes (epsilon-Muster [3]) oder spezieller Diskretisierungsmethoden (Sehnendreiecksnetze [4]) lässt sich bei Verfeinerung der polyedrischen Fläche Konvergenz nachweisen.
In der folgenden Abbildung ist ein optischer Vergleich der tatsächlichen Gaußkrümmung (links) und der Schätzung aufgrund obiger Formel (rechts) auf dem hyperbolischen Paraboloid zu sehen. Bei einer für die Diskretisierung gewählten Maschenweite von 1/32 lag bei dieser und anderen Quadriken eine maximale Abweichung von weniger als 1 Prozent vor.
 |
 |
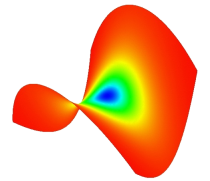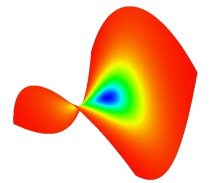Weitere Resultate
Ähnliche Ergebnisse lassen sich für die diskrete mittlere Krümmung beweisen [3]. Die Beweise verwenden den Begriff des Normal Cycle sowie Resultate aus der geometrischen Maßtheorie. Kurz sei auch noch auf die bekannten Resultate der Approximationstheorie hingewiesen, die besagen, dass bei lokaler polynomialer Interpolation die Krümmungsgrößen des Interpolanten gegen die der regulären Fläche konvergieren [5].
Literatur
[1] K. Hildebrandt und K. Polthier. Anisotropic Filtering of Non-Linear Surface Features. Eurographics 2004.
[2] L. Alboul. Optimising Triangulated Polyhedral Surfaces with Self-intersections. In Mathematics of Surfaces 2003, 48-72, Springer-Verlag, 2003.
[3] D. Cohen-Steiner and J.-M. Morvan. Restricted delaunay triangulations and normal cycle. In Proceedings of the nineteenth Conference on Computational Geometry (SCG-03), 312-321, San Diego, California, USA, 2003.
[4] R. Sauer. Differenzengeometrie. Springer-Verlag, 1970.
[5] F. Cazals und M. Pouget. Estimating Differential Quantities using Polynomial fitting of Osculating Jets. Technical report, Institut national de recherche en informatique et en automatique, 2003.