Kurzfassung

Die Arbeit beschäftigt sich mit Methoden zur Erzeugung glatter Oberflächen von Körpern mit beliebigem Genus. Da eine affine Parametrisierung von Oberflächen mit Genus g ≥ 2 nicht möglich ist, werden linear rationale Reparametrisierungen untersucht. Es wird beschrieben, wie man mit diesen eine projektive Struktur des Körpers erzeugt und wie man diese projektive Struktur nutzen kann, um die Oberfläche zu glätten. Außerdem werden Algorithmen und Methoden erläutert, die genutzt wurden, um all dies konkret zu realisieren. Zum Schluss werden die Ergebnisse analysiert und es wird untersucht, an welchen Stellen noch Verbesserungsbedarf besteht. Für die festgestellten Probleme werden Lösungsansätze diskutiert.

Linear rationale Reparametrisierungen

Untersucht wurden Funktionen der Form

##\rho(u,v)=\begin{pmatrix}\frac{a_1u+b_1v+c_1}{d_1u+e_1v+f_1} \\ \frac{a_2u+b_2v+c_2}{d_2u+e_2v+f_2}\end{pmatrix}##.

Die Reparametrisierung soll einige Eigenschaften erfüllen, die in der Arbeit festgelegt werden. Diese Restriktionen eliminieren die Freiheitsgrade. Zum Schluss bleibt die Funktion

##\rho(u,v)=\frac{1}{1+\tau_1v}\begin{pmatrix}-v \\ u+\tau_0v\end{pmatrix}##.

Projektive Strukturen

Diese Funktion wird dann als Kartenwechsel projektiver Strukturen verwendet. Es werden die projektiven Strukturen verschiedener Mannigfaltigkeiten generiert. Einige Beispiele finden sich unterhalb.

Ergebnisse

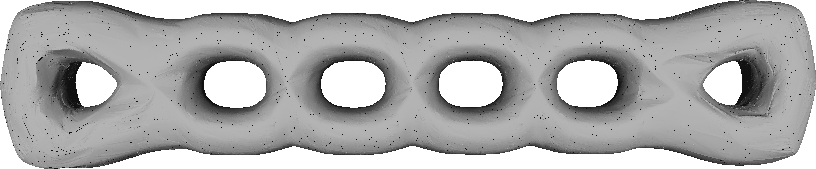
Mithilfe der projektiven Strukturen ist es dann möglich G¹ glatte Flächen zu erzeugen. Es folgen einige so erzeugte Flächen.