Optimale Flächenschnitte
- Type:Studienarbeit
- Date:2004
- Author(s):Nadja Klauß
- Links:.PDF
.BIB -
Ziel war es zu einer gegebenen bikubischen Bézier-Fläche F eine Richtung zu finden, die mit den Flächennormalen einen möglichst großen Winkel einschließt. Diese Richtung ist als Normale einer Ebenenschar E geeignet, deren Schnitte mit F die Kontur der Fläche optimal beschreiben.
Um dies zu erreichen, wurden zwei Verfahren implementiert und verglichen. Das eine Verfahren ist eine Abwandlung der in Farouki2002 vorgestellten Vorgehensweise. Hierbei wird zuerst, wie in Farouki2001 beschrieben, der Rand der symmetrischen Gaußabbildung durch einen Polygonzug angenähert. Anschließend wird die konvexe Hülle der Eckpunkte dieses Polygonzugs im dreidimensionalen Raum bestimmt. Auf der konvexen Hülle wird zunächst das Komplement S? des Normalenbereichs S von F bestimmt. In S? wird danach die Facette mit dem geringsten Abstand zum Ursprung bestimmt. Die Normale dieser Facette ist ein Ergebnis des Verfahrens.
Das andere Verfahren verzichtet darauf, den Rand der Gaußabbildung zu betrachten. Stattdessen wird das Parametergebiet der Fläche gleichmäßig abgestastet und die zugehörigen Normalen berechnet. Zu den Endpunkten der Nomalen auf der Einheitskugel werden noch die am Ursprung gespiegelten Punkte hinzugenommen. Von diesen Punkten wird die konvexe Hülle berechnet. Anschließend wird auf der konvexen Hülle die Facette mit dem geringsten Abstand zum Ursprung bestimmt. Auch hier ist die Normale dieser Facette ein Ergebnis.
Beide Verfahren wurden bezüglich Laufzeit und Ergebnissen verglichen. Beim Verfahren ohne Randberechnung erhöht sich die Laufzeit deutlich bei hohen Auflösungen. Der Vergleich der Ergebnisse zeigt jedoch, dass hohe Auflösungen meist nicht notwendig sind. Bei mittleren Auflösungen sind beide Verfahren etwa gleich schnell und auch die Ergebnisse weichen nur um wenige Grad voneinander ab.
Beim Vergleich der Ergebnisse mit dem Verfahren von Farouki stellt sich heraus, dass die Ergebnisse beider Verfahren nur um bis zu 4 Grad abweichen.
 |
 |
| Fläche entlang Höhenlinen ausgefräst Es sind deutliche Unebenheiten erkennbar.* |
Fläche ausgefräst entlang optimaler Schnittlinien Die Fläche weist kaum noch sichtbare Unebenheiten auf.* |
 |
|
| Endpunkte der Normalen und gespiegelte Punkte auf der Einheitskugel. Mit diesen Punkte wird beim Verfahren ohne Randbestimmung das Normalengebiet angenähert. |
|
 |
 |
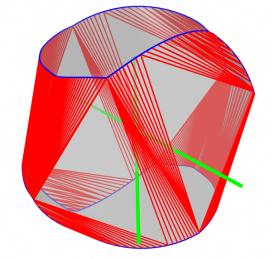
| Ergebnis des Verfahrens mit Randbestimmung Die blauen Kurven sind die Ränder des Normalengebiets S, die roten Linien die Kanten der konvexen Hülle die im Bereich von S? liegen und die grünen Linen sind die gefundenen Ergebnisse. |
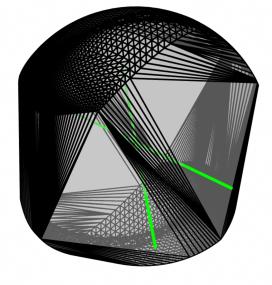
Ergebnis des Verfahrens ohne Randbestimmung Die schwarzen Linien sind die Kanten der konvexen Hülle, die grünen Linen die gefundenen Ergebnisse. |
* Diese Bilder stammen aus Farouki2002.
Literatur
- [Farouki2002] Tait S. Smith, Rida T. Farouki, Mohammad al-Kandari und Helmut Pottman, Optimal slicing of free-form surfaces, Computer Aided Geometric Design, 19, S.43-64, 2002
- [Farouki2001] Tait S. Smith und Rida T. Farouki, Gauss map computation for free-form surfaces, Computer Aided Geometric Design, 18, S.831-850, 2001
- [Samet1982] Hanan Samet, Neighborfinding Techniques for Images Represented by Quadtrees, Computer Graphics and Image Processing, 18, S.37-57, 1982
- [Barber1996] C. Bradford Barber, David P. Dobkin und Hannu Huhdanpaa, The Quickhull Algorithm for Convex Hulls, ACM Transactions on Mathematical Software, 22(4), S.469-483, 1996
