Thema dieser Diplomarbeit ist die Realisierung und Untersuchung eines Morphing-Verfahrens für dreidimensionale Objekte, das darauf basiert, Distanzfelder der beteiligten Objekte zu verwenden. D. h., es sollen Zwischenobjekte aus zwei in einer Netz-Darstellung gegebenen Modelle bestimmt werden, die einen homogenen Übergang vom Ausgangs- zum Endzustand repräsentieren. Berechnete Zwischenobjekte können zum einen direkt als facettiertes Netz exportiert werden, und zum anderen als Animation in einer gerenderten Ansicht die Verwandlung in ihrer vollen Dynamik demonstrieren lassen.

Im Mittelpunkt steht das diskretisierte Distanzfeld eines netzbasierten Objektes, welches über einem regelmäßigen dreidimensionalen Rastergitter aufgebaut wird. Alle Einträge (x,y,z) speichern den minimalen Abstand der dadurch spezifizierten Position zur Objektoberfläche, wobei das Vorzeichen des Wertes die Aussage zuläßt, ob der betreffende Punkt innerhalb oder außerhalb des Objekts liegt. Dabei wird die Verfahrensweise angestrebt, der exakten euklidischen Distanzmessung mit reellwertigen Abstandwerten möglichst nahe zu kommen. Der enorm hohe Rechenaufwand bei typischen Rasterfeldern mit etwa 200 x 200 x 200 (= 8 Mio.) Rasterelementen wird deshalb durch die Verwendung von Integer-Arithmetik und einem mit lokalen, optimierten Masken (Chamfer-Masken) operierenden Algorithmus zur Distanz-Transformation praxistauglich reduziert.

Das Grundverfahren ermittelt eine implizite Darstellung F des Zwischenobjektes zum Zeitpunkt 0 <= t <= 1 durch univariate Interpolation zwischen den Distanzfeldern DF1 und DF2 von Ausgangs- und Zielobjekt:

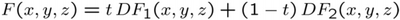
Aus F kann durch Iso-Flächenextraktion der Nulldurchgangs-Punkte (deren subvoxelgenaue Positionen durch trilineare Interpolation geschätzt werden) ein Netz mit Knoten und Facetten generiert werden (Marching-Cubes-Algorithmus).

Das beschriebene grundlegende Vorgehen funktioniert prinzipiell und liefert Ergebnisse, die wie folgt aussehen können:

Reines Distanzfeldmorphing ohne separate affine Transformation [MPG-Video, 183kb]

Typische Probleme zeigen sich durch verschwindende und sich dann neubildende Strukturen; Objekte können in mehrere Komponenten zerfallen und zeigen i. A. keine signifikante Ähnlichkeit mit den gegebenen Objekten.

Um dem entgegenzuwirken, werden im erweiterten Verfahren Bewegungen (Translationen) des Objektes und einfache affin beschreibbare Veränderungen (Drehungen, Streckungen in den Hauptachsen-Richtungen) als solche erkannt, deren Parameter bestimmt und schließlich eine affine Transformation abgeleitet, die eine Angleichung der beiden gegebenen Objekte aneinander erreicht. Diese Hauptachsen-Transformation wird interpolierend in die Verarbeitungskette zum Bestimmen eines Zwischenobjekts integriert. Damit erreicht man, dass Zwischenobjekte der Metamorphose

• eine Translation mit konstanter Geschwindigkeit von der Ausgangs- zur Zielposition ausführen,
• eine Drehung mit konstanter Winkelgeschwindigkeit und fester Drehachse beschreiben,
• sowie gleichförmig ablaufende Streckungen/Stauchungen in den drei Hauptachsenrichtungen aufweisen.

Die Metamorphose zwischen den gleichen Objekten wie oben läuft unter Hinzunahme der Hauptachsen-Transformation nun wie folgt ab:

Distanzfeldmorphing mit integrierter Hauptachsen-Transformationen [MPG-Video, 183kb]

Dennoch sind weiterhin Fälle zu beobachten, bei denen ungewollte Auflösungserscheinungen stattfinden, insbesondere bei Tiermodellen mit ausgeprägten Extremitäten. Um weitere Abhilfe zu verschaffen, wird eine zusätzliche Transformation realisiert, welche die affine Transformation verallgemeinert. Diese als elastische Transformation bezeichnete Verformung basiert auf paarweise vorgegebenen Ankerpunkten im Ausgangs- und Zielobjekt, die an markanten Positionen plaziert werden. (In dieser Arbeit wird dies durch eine Software-Schnittstelle erledigt, mit der der Benutzer Ankerpunkte in den 3D-Modellen exakt positionieren kann.)

Die auf diese Weise unregelmäßig verteilten Ankerpunktpaare definieren Interpolationsbedingungen für ein Problem der Scattered Data Interpolation. Die Interpolation in den Bereichen zwischen den Ankerpunkten wird letztlich mit dem Konzept radialer Basisfunktionen erreicht.

Distanzfeldmorphing mit integrierter elastischer Transformationen basierend auf 15 Ankerpunktpaaren [MPG-Video, 183kb]

Größeres Beispiel mit Metamorphosen von 13 Objekten ineinander [MPG-Video, 2,14mb]. Man betrachte das Video in einer Endlos-Schleife!