Die Rekonstruktion vollständiger dreidimensionaler Objekte ist ein wichtiges Forschungsgebiet der Computergraphik. In vielen Anwendungsgebieten der Bildverarbeitung liegen die Informationen über räumliche Objekte nur als ein Satz von zweidimensionalen Daten vor. Dies sind beispielsweise, die Schichtaufnahmen aus bildgebenden Verfahren der Medizin (CT, MRT) und Ansichten eines Objektes aus mehreren Kameraperspektiven. Je nach Aufgabenstellung kann die 3D-Rekonstruktion aus diesen Informationen unterschiedlich erfolgen: Bei den Schichtdaten werden die folgenden Zwischenschichten mit der gewünschten Genauigkeit linear oder bilinear interpoliert und die zweidimensionalen Pixel zu dreidimensionalen Voxeln ausgedehnt. Hier betrachten wir nur den zweiten Fall, in welchem die Oberflächen von in diesen Aufnahmen befindlichen Objekten rekonstruiert werden sollen.
Bei der Registrierung werden die vom Scanner gelieferten Ansichten des Objekts einander zugeordnet. Basierend auf diesen Zuordnungen wird ein Gesamtobjekt rekonstruiert. Die meisten Methoden der Registrierung versuchen das klassische Problem der absoluten Orientierung zu lösen: die Bestimmung der Transformation zwischen den Koordinatensystemen beider oder mehrerer Datensätze.
Der Standard-Algorithmus für die Registrierung ist der Iterative-Closest-Point-(ICP)-Algorithmus. Den ICP-Algorithmus kann man bei der Registrierung von verschiedenartigen geometrischen Objekten benutzen, wie zum Beispiel Punktmengen, Mengen von Kurven, Dreiecken oder parametrisierten Flächen.
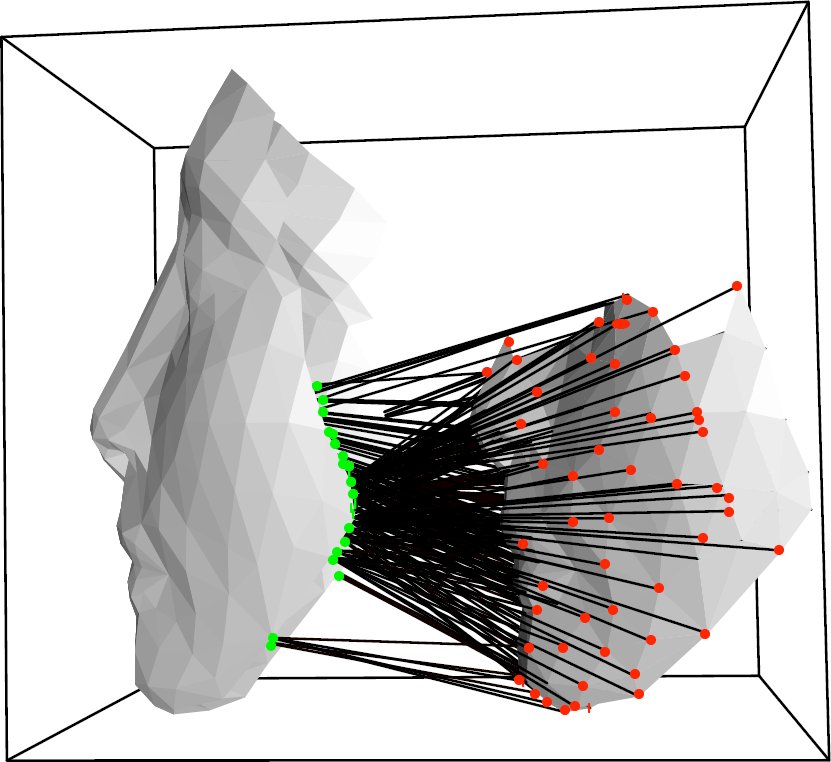
In dieser Arbeit wurde die Registrierung mehrerer Ansichten mit dem Trimmed-ICP-Algorithmus implementiert. Die Aufgabe der Registrierung ist es, die relative Position und Ausrichtung der einzelnen Aufnahmen zu finden. Es wird also versucht, die Daten in einen gemeinsamen Zusammenhang zu bringen, indem man jeweils die Transformation schätzt, welche die eine Aufnahme möglichst gut auf die andere abbildet. Ein erstes Problem besteht dann, wie man zu jedem Punkt aus einer Ansicht seinen nächsten Nachbarn in einer anderen Ansicht finden kann (siehe Abb. 1).
 |
| Abb. 1 |
Wir stellen ein Verfahren vor, mit dem man schneller die korrespondierenden Punkte auf triangulierten Oberflächen bestimmen kann. Um eine Schwäche des originalen ICP-Algorithmus auszugleichen, wurde eine Variante des ICP-Algorithmus benutzt, der so genannte Trimmed-Iterative-Closest-Point (TriICP) Algorithmus. Dabei wurden zwei Methoden verwendet, um die Überlappungsbereiche zwischen zwei Ansichten zu definieren (siehe Abb. 2). Mit dieser Teilmenge der Punktpaarung wurden dann, genau wie im ICP-Algorithmus, die Registrierungsvektoren berechnet.
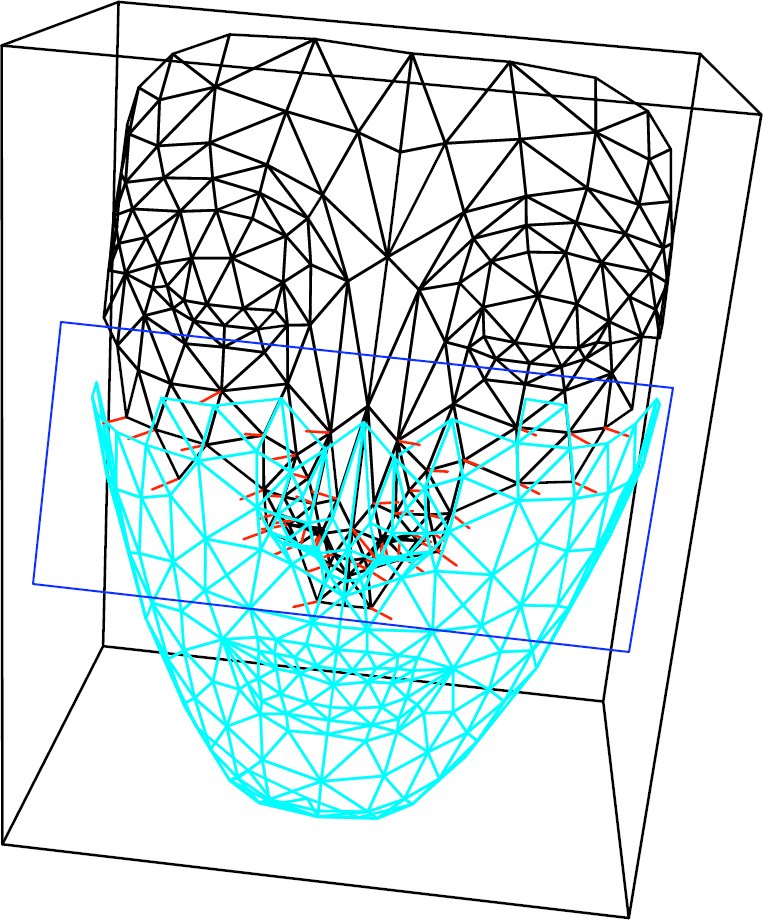 |
| Abb. 2 |
Weiterhin wurde die Registrierung mehrerer Ansichten durch einen globalen Registrierungsalgorithmus realisiert.
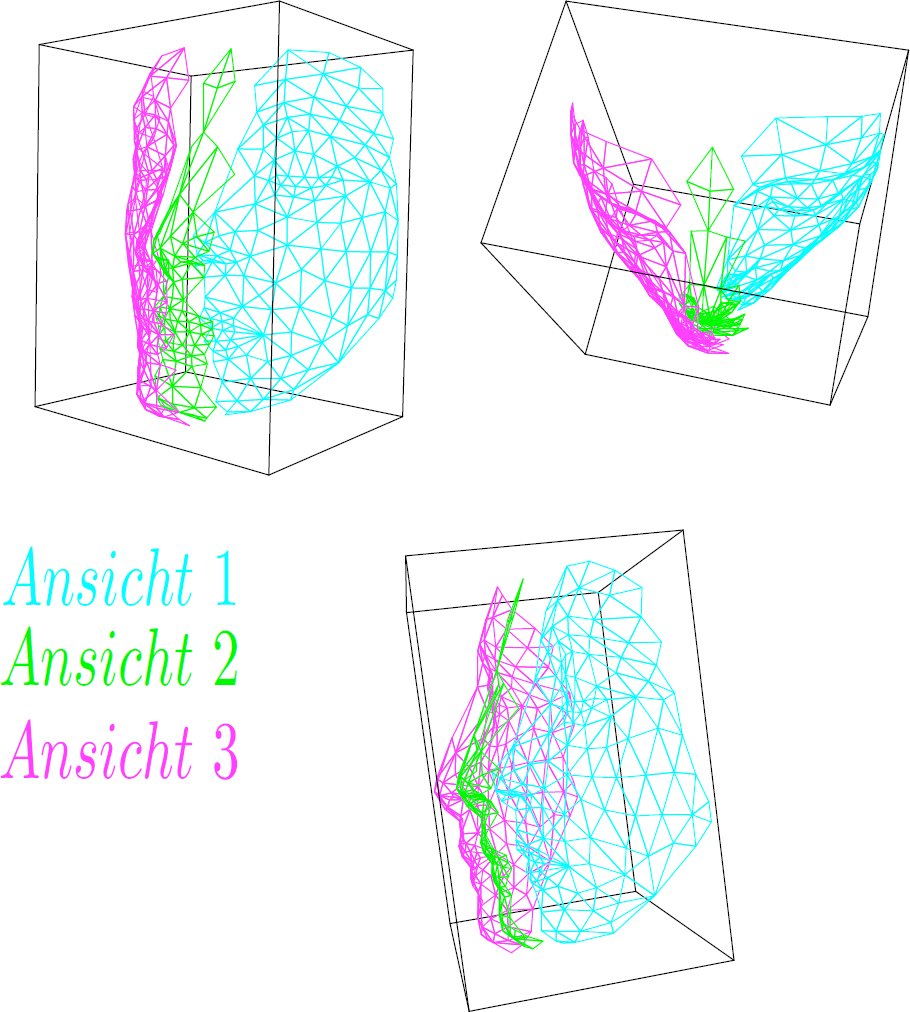
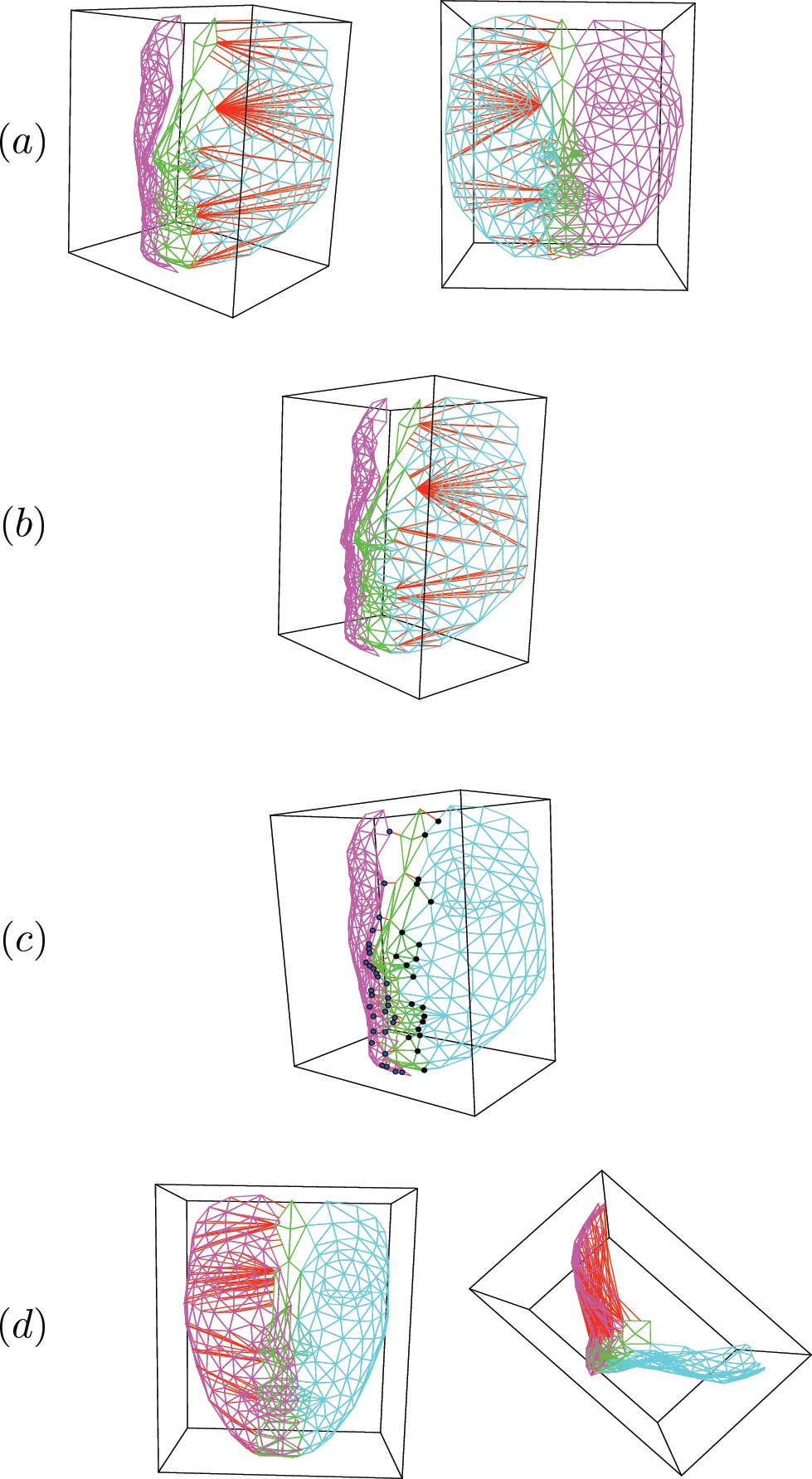
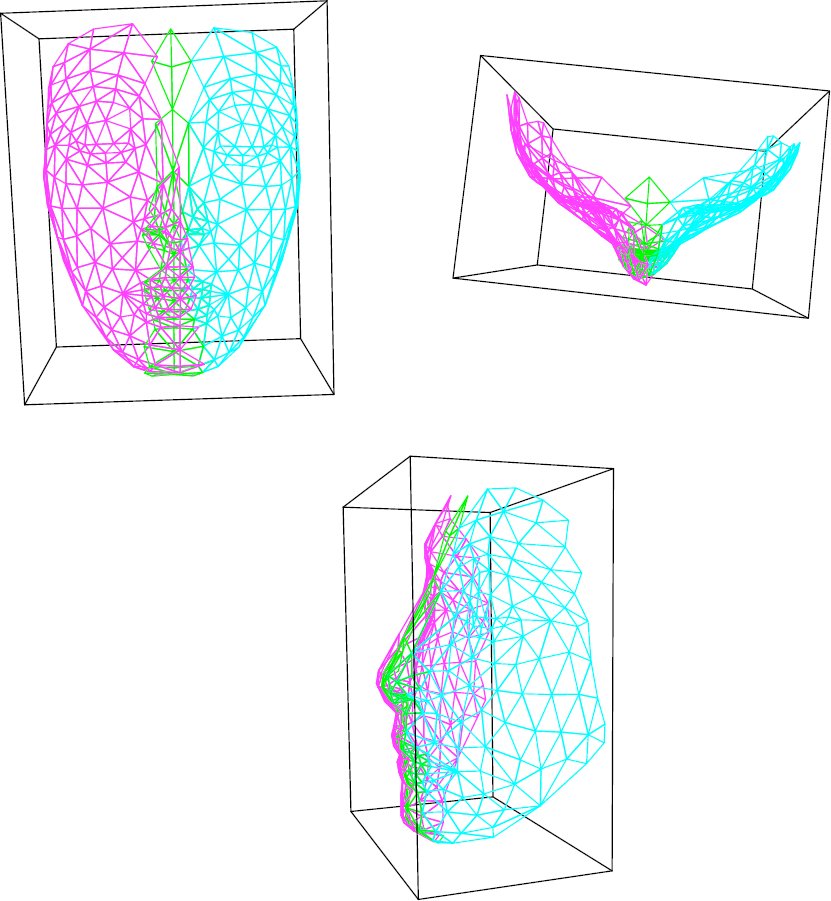
Die Registrierung mehrerer Ansichten zeigen wir anhand eines Beispiels mit drei Ansichten (siehe Abb. 3). In die Abbildung 4(a) bestimmen wir zunächst zu jedem Punkt aus Ansicht 1 seinen korrespondierenden Punkt in Ansicht 2. Abb. 4(b) zeigt uns das Ergebnis nach der Registrierung von Ansicht 1 und Ansicht 2. Danach wird zu jedem Punkt aus Ansicht 2 sein korrespondierender Punkt in seinen Nachbaransichten (Ansicht 1 und Ansicht 3) bestimmt (siehe Abb. 4(c)). Nach der Registrierung von Ansicht 2 und seinen Nachbaransichten (neue Ansicht 1 und Ansicht 3) bestimmen wir zu jedem Punkt aus Ansicht 3 seinen korrespondierenden Punkt in Ansicht 2 (siehe Abb. 4(d)). Zum Schluss erhalten wir das Ergebnis der Registrierung dieser drei Ansichten (siehe Abb. 5).