In der heutigen Zeit werden dreidimensionale Computermodelle immer komplexer. Dies liegt daran, dass die heutigen Rechner leistungsfähiger sind und man somit mehr Daten verarbeiten kann und die Techniken zum Gewinnen eines dreidimensionalen Modells, wie z. B. mit Hilfe eines 3D-Scanners, immer ausgefeilter werden. Will man jedoch diese Modelle in Echtzeit darstellen, muss oft die Komplexität des Modells reduziert werden.

Doch nicht nur für die Darstellung der Modelle ist eine Reduktion der Daten notwendig, auch für andere Anwendung kann dies sinnvoll sein. So wurde z. B. in einer anderen Studienarbeit ein Verfahren vorgestellt, um aus einem 3D-Modell einen Bastelbogen generieren zu können, mit dem man das 3D-Modell aus Papier nachbauen kann. Da bei einem Bastelbogen Modelle mit zu vielen Kanten unbrauchbar werden, muss eine starke Reduktion der Daten durchgeführt werden. Zusätzlich muss man sich Gedanken machen, wie die Texturen des vereinfachten Netzes sein müssen, damit das vereinfachte Modell dem komplexen Modell möglichst ähnlich ist. Leider stellt man auch schnell fest, dass die meisten 3D-Modelle gewisse Anforderungen, die man zum Vereinfachen braucht, nicht haben.

Ziel dieser Arbeit war es, Modelle zu reparieren, damit sie bestimmten Anforderungen genügen, die Modelle danach zu vereinfachen und diese mit neuen Texturen zu versehen und dabei das Aussehen so nah wie möglich am ursprünglichen Modell zu halten.

Reparatur

Da 3D-Modelle beim Konvertieren zwischen unterschiedlichen Datenformaten oft in mehrere Netze aufgetrennt werden,ist es wichtig, diese vor der Vereinfachung wieder zusammenzufassen. So wurde z. B. das Modell des Karlsruher Schlosses von 1160 zu 193 Netzen zusammengefasst.

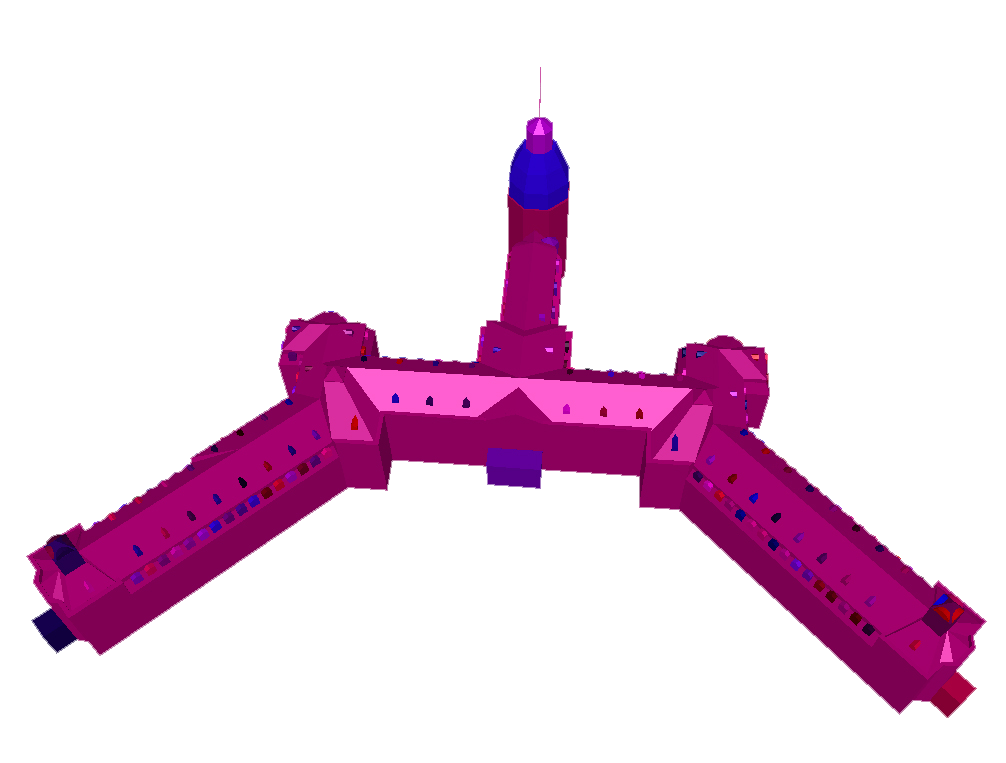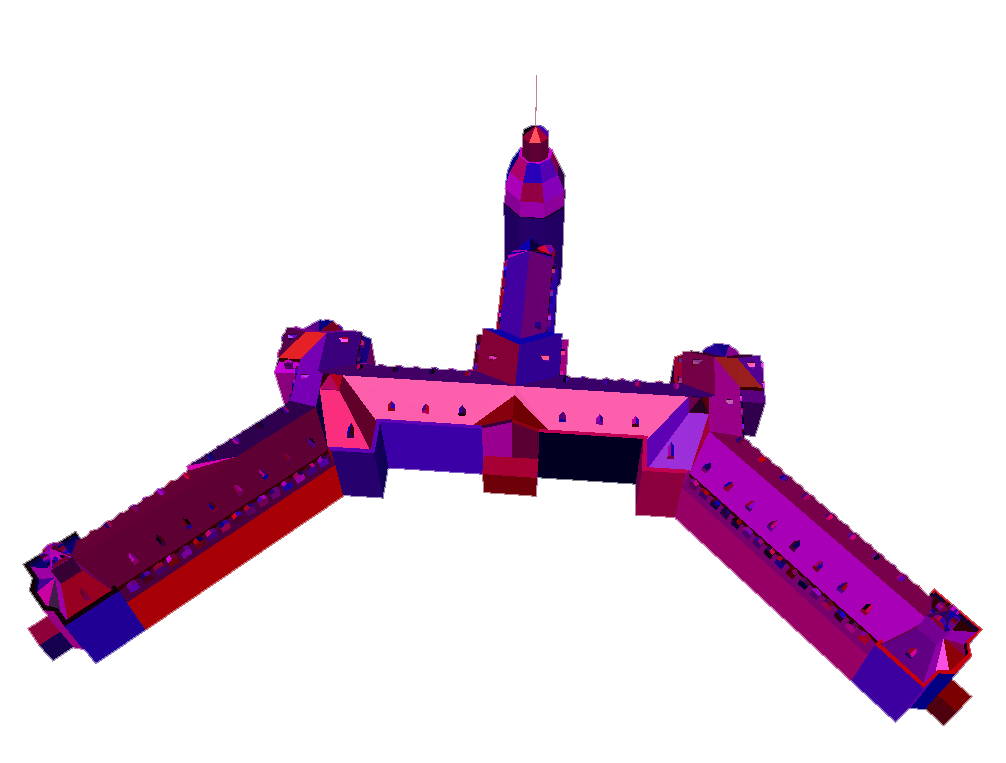
Zusammenfassen der Netze eines Modells zu größeren Netzen: Unterschiedliche Netze werden mit unterschiedlichen Farben dargestellt.

In einem weiteren Schritt müssen die Netze in mannigfaltige Netze überführt werden. Hierfür wurde ein einfacher Algorithmus implementiert, der anhand lokaler Entscheidungen Kanten und Ecken des Netzes auftrennt. Hierdurch können Löcher entstehen, die wieder neu trianguliert werden müssen.

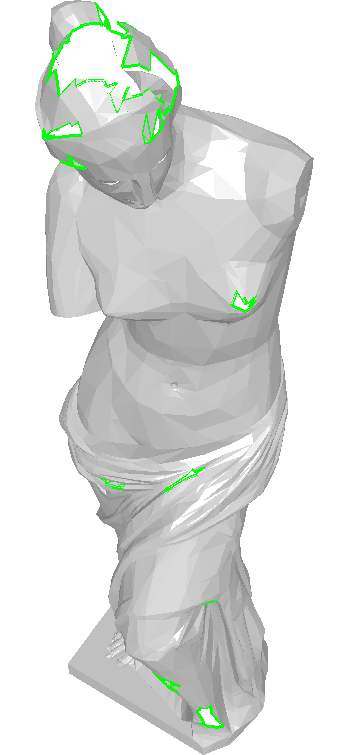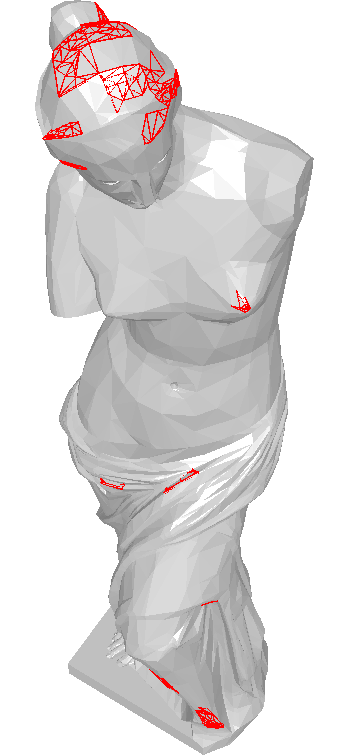
Löcher nach dem Überführen in ein mannigfaltiges Netz: Ein Modell mit vielen rot markierten Nicht-Mannigfaltigkeiten (links) wird aufgetrennt. Es entstehen die grün markierten Löcher (rechts).

Zusätzlich werden in den Netzen doppelte Facetten gelöscht, nahe beieinander liegende Ecken zusammengefasst und alle Netze konsistent orientiert.

Vereinfachung

Um die Netze zu vereinfachen, wurde ein Algorithmus implementiert, der anhand von Abstands-, Krümmungs- und Verzerrungskriterien des Netzes iterativ Kanten zusammenzieht, um so die Anzahl der Facetten zu reduzieren. Unterschiedliche Gewichtungen der Kriterien wirken sich beim Vereinfachen unterschiedlich aus. Zusätzlich wurden beim Vereinfachungsalgorithmus überprüft, dass ein Vereinfachungsschritt zu keiner Selbstdurchdringung des vereinfachten Netzes führt.

Resultate der Netzvereinfachung: Das ursprüngliche Modell (links oben) wurde vereinfacht, wobei Wert auf Krümmungserhaltung (rechts oben), auf gleichmäßige Dreiecke (links unten) und auf möglichst geringe Abweichung des vereinfachten Netzes (rechts unten) gelegt wurde.

Projektion des ursprünglichen Netzes auf das vereinfachte Netz

Da sich das Aussehen des vereinfachten Netzes von demjenigen des ursprünglichen Netzes unterscheidet, wird das ursprüngliche auf das vereinfachte Netz projiziert. Um kleine Details der Oberfläche sichtbar machen zu können, wurde zusätzlich ein approximatives Ambient-Occlusion-Beleuchtungsmodell implementiert.

Gerendertes Modell: hinten das usprüngliche Netz, vorne das vereinfachte Netz mit projizierter Textur.

Vereinfachung des Stanford Bunnys (hinten): Auf das vereinfachte Netz wurde eine Textur projiziert (vorne), die mit Hilfe eines approximativen Beleuchtungsmodells auf dem ursprünglichen Netz berechnet wurde.