Geodätische Kurven einer regulären Fläche lassen sich als eine Verallgemeinerung von Geraden des Euklidischen Raumes auffassen. Sie sind gegeben durch die Spuren beschleunigungsfreier Bewegungen und kürzester Verbindungen zwischen je zwei Punkten einer Fläche. Ausgehend von Betrachtungen dieser Kurven auf Flächen und Netzen, werden in dieser Arbeit Verfahren entwickelt und nachvollzogen, mit denen sie sich auf Punktwolken bestimmen lassen.

Zum einen wurde ein Verfahren entwickelt, mit dem sich beschleunigungsfreie Pfade auf Punktwolken mit Hilfe partieller Dreiecksnetzgenerierung bestimmen lassen. Zum anderen wurde eine Idee von F. Memoli und G. Sapiro [1,2] ausgearbeitet, die kürzesten Verbindungen auf einer Fläche, die durch eine Punktwolke gegeben ist, über die Fast-Marching-Methode innerhalb einer Tubenumgebung der Fläche anzunähern.

Eine Punktwolke wird lokal mit Paraboloiden approximiert, und mit Hilfe dieser Informationen in eine Fächerwolke überführt. Somit lässt sie sich wie ein Dreiecksnetz schattiert darstellen.

Mit den so gewonnen Informationen lassen sich auf einer Punktwolke beschleunigungsfreie Pfade bestimmen, indem man sie dort in ein topologisch korrektes Dreiecksnetz überführt, wo es für die Verfolgung dieser Linien notwendig ist. Durch Generieren von Punktwolken aus parametrisierten Flächenstücken, lassen sich die auf Punktwolken bestimmten Pfade mit den Geodätischen der Fläche vergleichen; die Geodätischen einer Fläche erhält man mit dem Runge-Kutta-Verfahren zur Lösung von Systemen aus Differentialgleichungen erster Ordung. In den unteren Grafiken sind die sozusagen exakten Geodätischen dick und die Pfade auf der Punktwolke dünn gezeichnet. Man erkennt durch Überlagerung, dass die im Rahmen dieser Arbeit entwickelten Linien auf unregelmäßigen Punktwolken die geodätischen Kurven regulärer Flächen besser annähern (linkes Bild), als die von Polthier und Schmies [3] eingeführten direktesten Geodätischen (rechtes Bild).

Für die Bestimmung kürzester Verbindungen auf einer Fläche wurde ein Ansatz von Memoli und Sapiro nachvollzogen. Dabei wurde gezeigt, unter welchen Voraussetzungen die kürzesten Verbindungen innerhalb einer Tubenumgebung der Fläche, die entsprechenden Kurven auf der Fläche annähern. Eine Tubenumgebung ist dabei festgelegt durch eine zusammenhängende Menge regulärer Parallelflächen einer regulären Fläche. Kennt man nun innerhalb einer solchen Teilmenge O des dreidimensionalen euklidischen Raumes eine Funktion T, die jedem Punkt von O, die Entfernung zu einem zu wählenden Saatpunkt p zuordnet, so sind die kürzesten Verbindungen bezüglich p durch die Trajektorien des Gradienten von T gegeben und es gilt || grad T || = 1. Diese partielle Differentialgleichnung heißt Eikonal-Gleichung und lässt sich mit Hilfe der von Sethian [4] beschriebenen Fast-Marching-Methode auf einem regelmäßigen Gitter in O - mit einem einzigen Gang darüber - näherungsweise lösen.

In dieser Arbeit wurde gezeigt, wie sich mit approximierenden Paraboloiden eine ausreichend dünne Tubenumgebung zu einer Fläche bestimmen lässt, von der nur eine Punktwolkenrepräsentation bekannt ist. Um die Fast-Marching-Methode auf diese Umgebung anzuwenden, ist zu beachten, dass ein Reduzieren der Dicke der Tubenumgebung auf 1/n-tel ihre Laufzeit um einen Faktor O(n²) verlängert, ein entsprechendes Reduzieren der Gitterweite gar um O(n³).

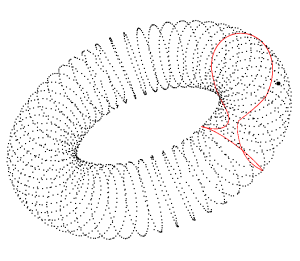
In den unteren Bildern ist dargestellt, wie für eine Toruspunktwolke mit 2550 Punkten kürzeste Verbindungen berechnet werden. Die beiden Bilder zeigen eine Front der von der Fast-Marching-Methode verwendeten Gitterpunkte beim Gang über das Gitter. Es ist zu erkennen, wie dünn sich eine Tubenumgebung der Fläche bestimmen lässt.

Die nächste Grafik zeigt den aus dem Gradienten bestimmten kürzesten Pfad, der von einer manuell bestimmten, beschleunigungsfreien Linie abgekürzt wird.

 

 

Der hierbei auftretende Fehler ist auf die Fast-Marching-Methode zurückzuführen, wie das nächste Bild zeigt. Dazu wurde für eine Ebene die Funktion T und ihr Gradient angenähert. Die gebogene Kurve folgt diesem Gradienten, ist aber natürliche keine kürzeste Verbindung auf einer Ebene.

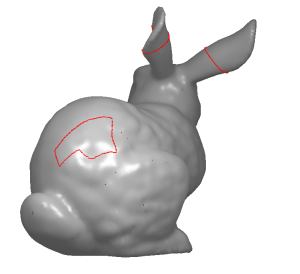
Die drei letzten Grafiken zeigen, dass sich auch für komplexere Flächen ausreichend dünne Tubenumgebungen bestimmen lassen und beinhalten eine Visualisierung der mit der Fast-Marching-Methode bestimmten Funktion T. Dabei wurden für ausgewählte Werte von T die Punkte schwarz gezeichnet, um Isolinien der Funktion nachzuahmen.

 

[1] F. Memoli und G. Sapiro, Distance Funtions and Geodesics on Point Clouds, Institute for Mathematics and its Applications, University of Minnesota, 2003
[2] F. Memoli und G. Sapiro, Fast Computation of Weighted Distance Functions and Geodesics on Implicit Hyper-Surfaces, Journal of Computational Physics, 173, Nr. 2, S. 730-764, 2001
[3] Konrad Polthier und Markus Schmies, Straightest geodesics on polyhedral surfaces, In H.C. Hege und K. Polthier (Hrsg.), Mathematical Visualization: Algorithms, Applications, and Numerics, S. 135-150, Springer, 1998
[4] James A. Sethian, Level Set Methods and Fast Marching Methods, 2. Auflage, Cambridge University Press, 1999