Übersicht
Diese Studienarbeit widmet sich der Untersuchung eines neueren Algorithmus zur Krümmungsapproximation von Flächen. Dieser benutzt die geometrische Algebra, um Krümmungskreise in verschiedenen Richtungen zu schätzen. Mit diesen Daten und Eulers Formel für die Normalkrümmung können dann die Hauptkrümmungen bestimmt werden.
Die Studienarbeit gibt einen kurzen Einblick in die geometrische Algebra, eine 5-dimensionale konforme Algebra, in der geometrische Objekte wie Punkte, Kugeln oder Ebenen einfach dargestellt werden können. Anschließend wird die Kugelapproximation durch die geometrische Algebra untersucht. Diese bildet die Grundlage für die Approximation der Krümmungskreise. Anschließend wird die Krümmungsapproximation kurz vorgestellt und mit der mathematisch exakten Krümmung sowie dem Verfahren von Taubin verglichen.
Ergebnisse
 |
 |
 |
 |
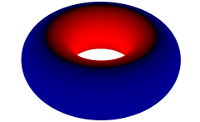
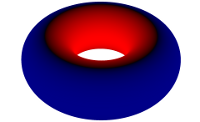
| Einige Testobjekte mit exakter gaußscher Krümmung |
|
 |
 |
 |
 |
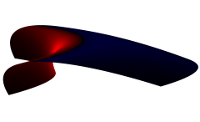
| Krümmungen nach Taubin |
|
 |
 |
 |
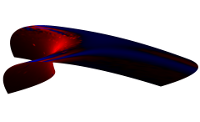 |
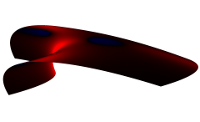
| Krümmungen mit geometrischer Algebra |
|
Ausblick
Auch wenn die Kugelapproximation verrauschte Kugeln nicht wirklich gut rekonstruieren konnte, so überraschte die Krümmungsapproximation dann bei einigen Flächen doch mit brauchbaren Ergebnissen. Wie man sieht wird die Krümmung allerdings nicht bei allen getesteten Objekten zufriedenstellend approximiert. Hier ist noch einiges an Arbeit notwendig. Allerdings ist nicht klar, ob das Verfahren mit kleinen Anpassungen und Tricks noch verbessert werden kann oder ob durch die vielen Approximationsschritte und das nicht intuitive Abstandsmaß der geometrischen Algebra das Verfahren hier schon an seine Grenzen gelangt ist.
