Die manuelle Modellierung von realistisch wirkenden Deformations- und Bruchvorgängen in computergenerierten Animationen ist sehr aufwendig und führt oft nicht zu den gewünschten Ergebnissen. Daher werden Simulationsalgorithmen eingesetzt, mit deren Hilfe solche Phänomene automatisch modelliert werden können.
In dieser Arbeit werden Simulationsverfahren vorgestellt, die bei akzeptablem Aufwand plausibel wirkende Ergebnisse erzeugen können. Dazu werden die gebräuchlichen Materialmodelle aus der Kontinuumsmechanik herangezogen und erläutert. Außerdem wird die Entstehung und Ausbreitung von Rissen genauer betrachtet. Verschiedene Ansätze, die aus diesen Modellen entstandenen kontinuierlichen Differentialgleichungen in Simulationsalgorithmen numerisch handhabbar zu machen, werden vorgestellt. Die speziellen Anpassungen dieser Deformationsmodelle, die nötig sind, um Brüche zu modellieren, werden aufgezeigt. Weiterhin werden verschieden Möglichkeiten zur Zeitintegration erläutert und auf ihre Vor- und Nachteile hin überprüft.
Basierend auf diesen Grundlagen wird ein bestehendes Verfahren modifiziert, das linear-elastische und plastische Deformationen sowie Brüche von homogenen und isotropen Materialien simulieren kann. Dieser Algorithmus verwendet die Finite Elemente Methode zur numerischen Diskretisierung und eine implizite Zeitintegrationsmethode.

Bei der Untersuchung der Simulationsergebnisse zeigt sich, dass ein weiter Bereich von Materialverhalten realistisch modelliert werden kann. Durch die implizite Zeitintegration können deutlich größere Zeitschritte stabil berechnet werden. Es zeigt sich, dass dadurch eine Beschleunigung des Simulationsvorgangs erreicht wird.

Das implementierte Simulationsverfahren verwendet ein in der Kontinuumsmechanik gebräuchliches Materialmodell, um Deformationen und die durch diese hervorgerufenen Spannungen zu berechnen. Dabei wird der undeformierte Körper in Referenzkoordinaten beschrieben, die durch eine Transformationsfunktion in Weltkoordinaten übertragen werden. Durch diese Transformation kann der Körper auch deformiert werden. Die dadurch entstehenden mechanischen Spannungen sind materialabhängig und werden durch eine Verallgemeinerung des Hookeschen Gesetzes aus der Deformation ermittelt.

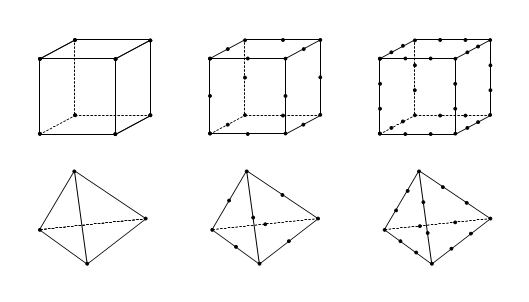
Quader- und Tetraederförmige Elemente unterschiedlichen Grades.

Um das kontinuumsmechanische Materialmodell numerisch berechenbar zu machen, ist der Einsatz eines Diskretisierungsverfahrens notwendig. In dieser Arbeit kommt dazu die Finite Elemente Methode (FEM) zum Einsatz. Bei der FEM wird das als kontinuierlich angenommene Material in diskrete Elemente unterteilt, die über auf den Elementkanten liegenden Knoten miteinander verbunden sind. Deformationen ergeben sich nun an den Knoten durch deren Verschiebungen, innerhalb der Elemente werden sie durch Basisfunktionen interpoliert. Diese Basisfunktionen sind meist Polynome, deren Grad durch die Anzahl der Knoten auf einer Kante bestimmt wird. Der implementierte Algorithmus verwendet aus naheliegenden Gründen tetraederförmige Elemente mit linearen Basisfunktionen.

Die Referenzkonfiguration eines Körpers u wird durch eine Transformationsfunktion x(u) deformiert.

Externe Kräfte, wie z.B. Kollisionen, und interne, durch Spannungen im Material induzierte Kräfte wirken auf den Körper ein. Die daraus resultierenden Bewegungen werden durch die Newtonschen Bewegungsgleichungen beschrieben, die in dieser Arbeit durch das linearisierte implizite Eulerverfahren gelöst werden. Dadurch können sehr steife Materialien über große Zeitschritte stabil berechnet werden.

 

Bruchsimulation am Beispiel eines Fensters, das durch einen Ball zerbrochen wird.

Durch lokale Veränderungen der Materialparameter lässt sich der Bruchvorgang falls gewünscht beeinflussen.