Zunächst werden grundlegende Definitionen zur Medialen Achse und den damit verbundenen Begriffen Voronoi-Diagramm und Cut Locus geliefert. Zudem werden einige wichtige Eigenschaften der Medialen Achse analysiert. Eine der Definitionen besagt, dass die Mediale Achse eines Körpers der Abschluss der Mittelpunkte maximal einschreibbarer Kugeln in den Körper ist.
Es werden verschiedene Algorithmen zur exakten Berechnung der Medialen Achse von Polygonen vorgestellt. Konvexe Polygone, simple Polygone als auch Polygone mit Loch werden betrachtet.
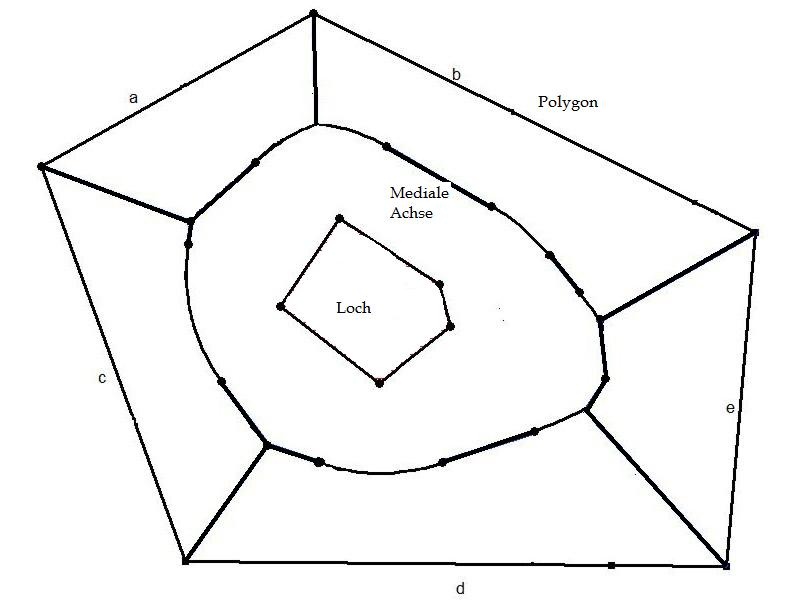 |
| Abbildung 1: Mediale Achse eines konvexen Polygons mit konvexem Loch |
Des Weiteren werden grundlegenden Überlegungen bezüglich der Medialen Achse eines Polyeders angestellt. Dabei spielen Bisektoren bezüglich der Begrenzungselemente eine wesentliche Rolle.
Zwei Programmierungen werden in der Arbeit vorgestellt. Zum Einen ein mit der Programmiersprache Delphi verfasstes Programm, welches die Mediale Achse eines konvexen Polygons berechnet und graphisch ausgibt. Zum Anderen ein Programm, welches mit der Programmiersprache Python erstellt wurde. Dieses Programm vermag es, die Mediale Achse eines gegebenen dreidimensionalen Körpers mit einer beliebig großen Zahl von Punkten zu approximieren. Die grundlegenden Ideen und die wichtigsten Funktionen werden dabei analysiert.
 |
| Abbildung 2: Approximierte mediale Achse eines Würfels mit ausgeschnittener Kugel in der Mitte |
Des Weiteren vermittelt diese Arbeit einen Einblick in die verschiedenen Anwendungen der Medialen Achse, diese kann in vielen Bereichen sehr nützlich sein. Näher eingegangen werden dabei unter anderem auf die Einsätze der Medialen Achse bei Probabilistic Roadmap Plannern im Bereich der Robotik und im Bereich der Computergrafik bei der Formenerkennung und der Formenreduktion. Es ist stets abzuwägen, ob eine exakte Darstellung gewünscht ist, oder eine Approximation reicht. Auch darauf wird eingegangen.
