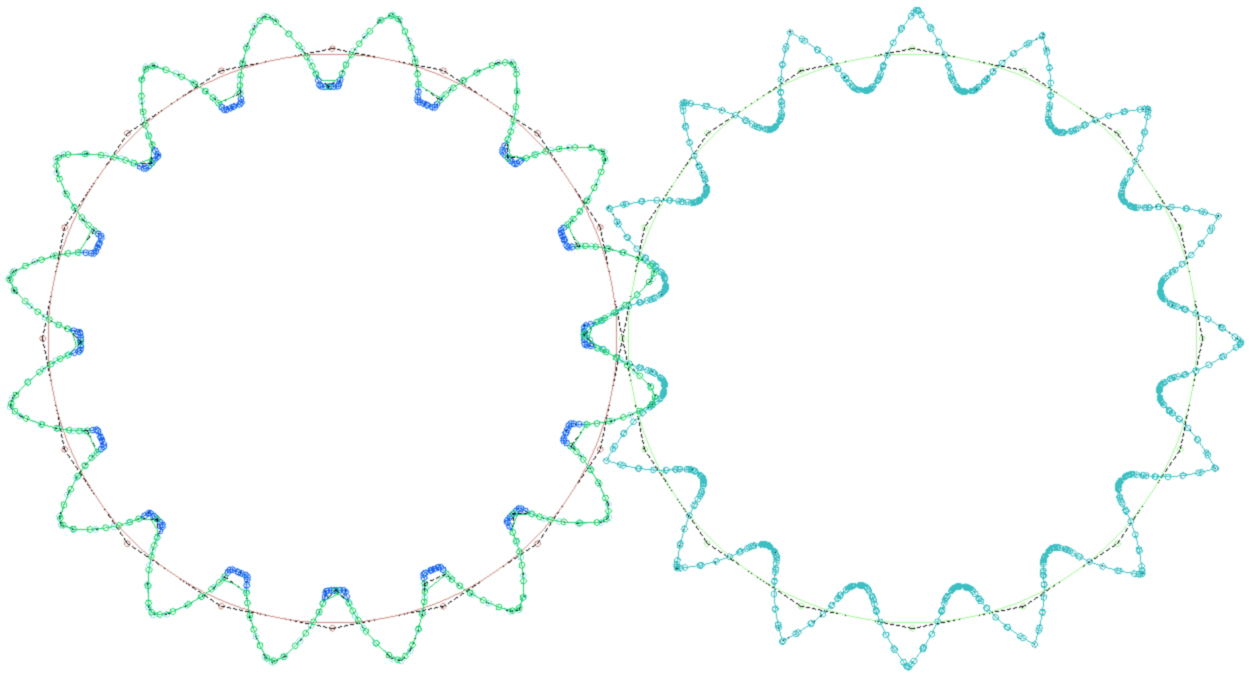
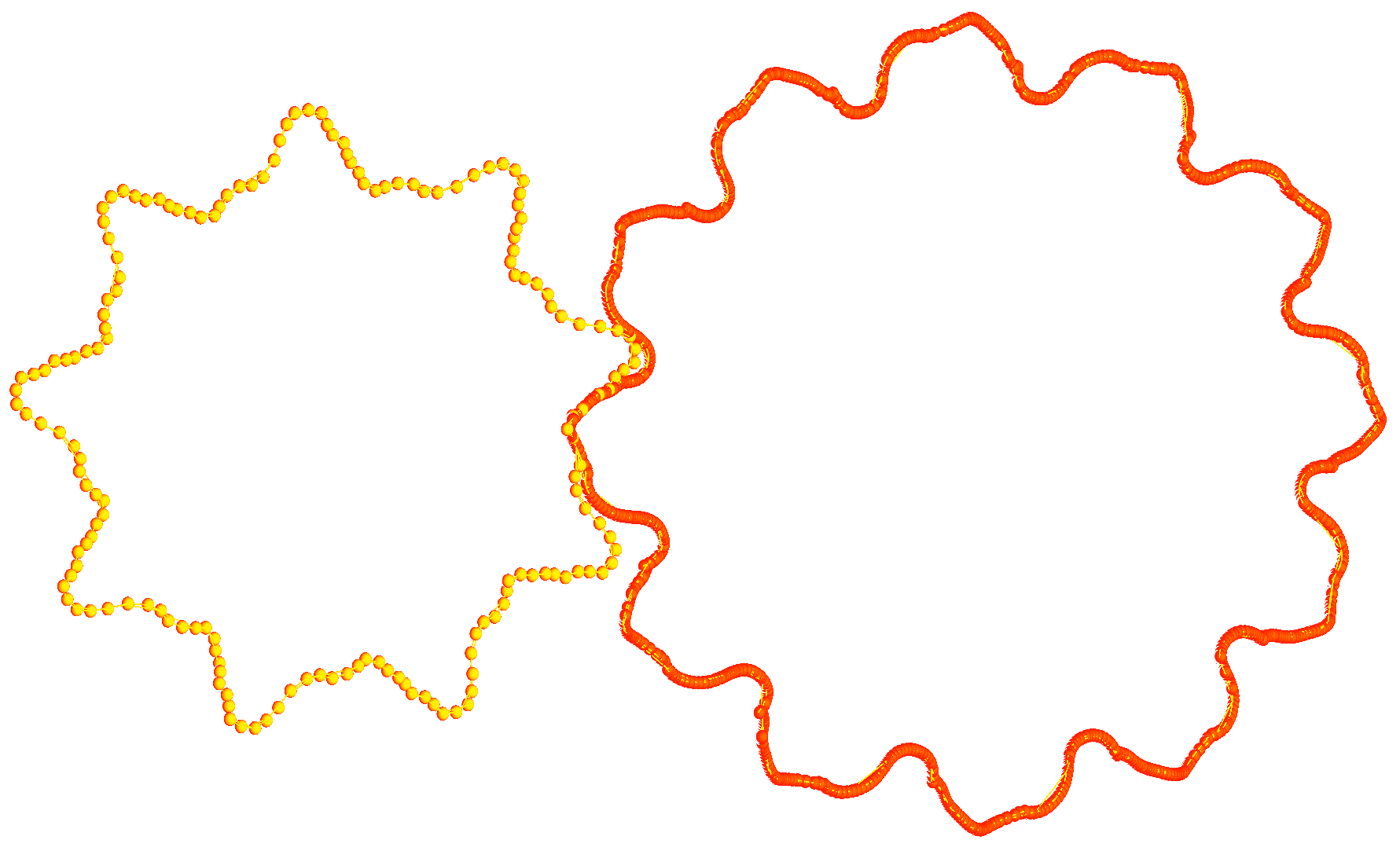
Obwohl Zahnräder schon sehr lange existieren, sind sie auch heute noch nicht wegzudenken aus vielen Maschinen und Getrieben. Die Arbeit gibt eine Einführung in die Verzahnungstheorie, indem zunächst das Verzahnungsgesetz hergeleitet wird. Anschließend werden einige der heute gebräuchlichen Verzahnungen vorgestellt und untersucht: die Kreisbogenverzahnung, die Wildhaber-Novikov-Verzahnung, die Zykloidenverzahnung und die Evolventenverzahnung. Für letztere wird eine Funktion für das Bezugsprofil und für ein Stirnrad hergeleitet, die im Happah-Projekt implementiert wurden.

Anhand des Verzahnungsgesetzes und der darauf aufbauenden Konstruktion von Reuleaux wird untersucht, wie zu beliebig vorgegebenen Treibrädern ein Gegenrad konstruiert werden kann. Das Programm nutzt zur Gegenradkonstruktion zusätzlich auch noch für jeden Punkt die Normalenrichtung und die Dicke des gegebenen Treibrads entlang dieser Normalen. In der Implementierung hat der Nutzer die Möglichkeit, eine beliebige Spline-Kurve (B-Spline) in der Ebene zu definieren, aus der ein Zahnrad erstellt wird. Für das Gegenrad kann dann die gewünschte Zähnezahl angegeben werden und es können im Anschluss die einzelnen Schritte, die zur Gegenradkonstruktion nötig sind, dargestellt werden.