Interaktive Simulationen für deformierbare Körper werden mit steigenden Rechenkapazitäten immer wichtiger in den Bereichen der Spiele- und Filmindustrie wie auch in der Medizin. Durch die Verwendung von physikalisch plausiblen Berechnungen gewinnt jede dieser Anwendungen ein hohes Maß an Realismus. Eine wichtige Komponente der dynamischen Simulation ist die Kollisionserkennung und -auflösung.
Die vorliegende Arbeit beschäftigt sich mit dem Verfahren der Kollisionserkennung durch Raumunterteilung von Teschner in [1]. Dieses Verfahren wurde implementiert und angepasst. Als Kollisionsgeometrie wird ein deformierbares Tetraedernetz verwendet. Diese Diplomarbeit stellt Verbesserungen vor, die in komplexen Szenen einen deutlichen Geschwindigkeitsvorteil erbringen. Dabei wird für jeden deformierbaren Körper eine eigene Hashtabelle verwendet und eine zusätzliche Eingrenzung des Kollisionsraums verringert die Anzahl der Kollisionstests. Des Weiteren wird für die Berechnung der Kollisionsinformationen auf die Arbeit von Heidelberger [2] zurückgegriffen und diese weiterentwickelt.
Das Ziel dieser Arbeit ist es, die Verfahren anzupassen und zu verbessern, da für jeden Simulationsschritt so wenig Rechenzeit wie möglich verwendet werden soll, um eine echtzeitnahe interaktive Simulation zu gewährleisten. 

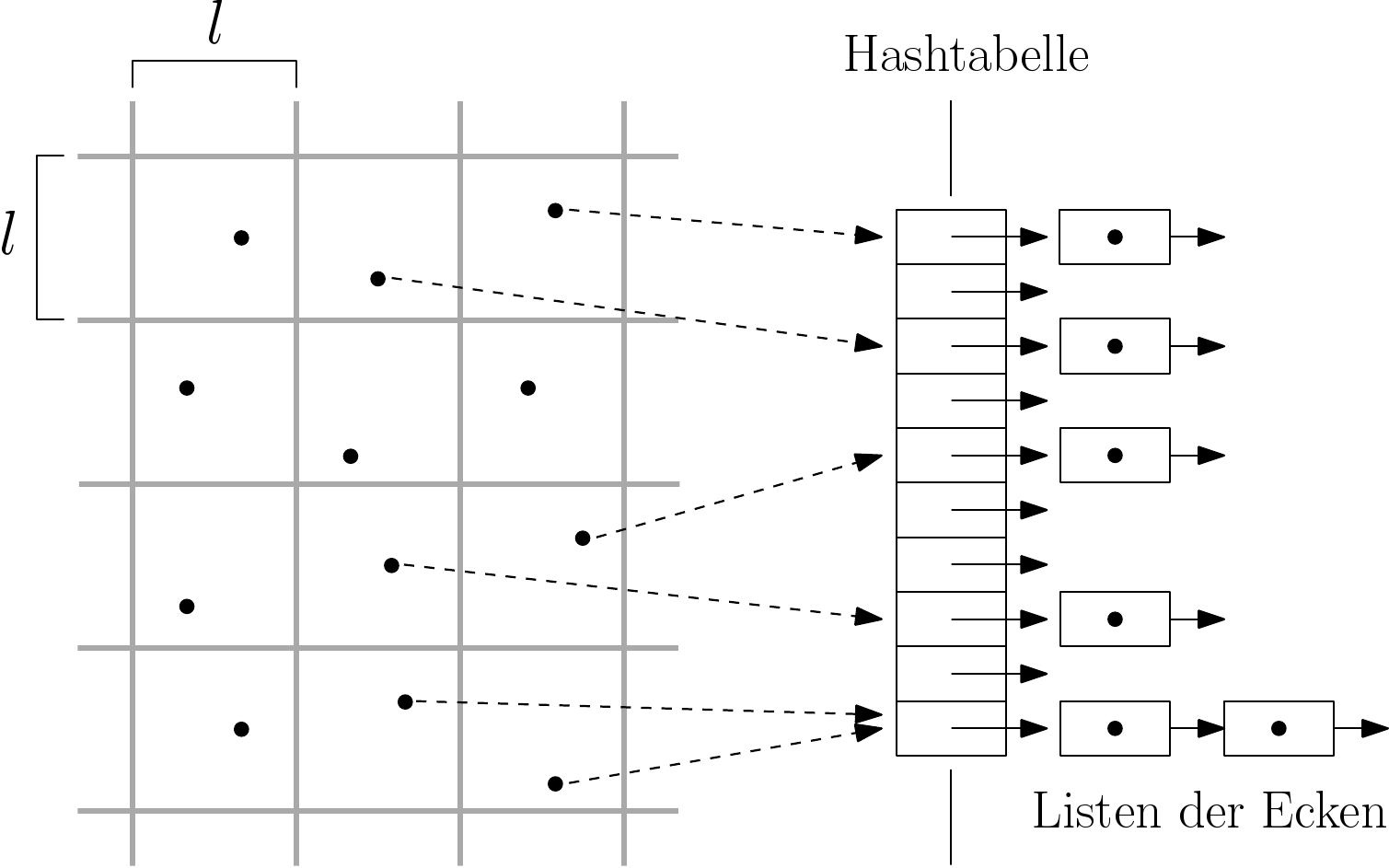
Das grundlegende Prinzip der Kollisionserkennung besteht darin, die Szene räumlich durch ein 3D-Gitter mit gleichgroßen Quadern zu unterteilen, wobei die Kantenlänge eines Quaders der durchschnittlichen Kantenlänge der Tetraeder entspricht, und die Ecken aller Tetraeder diesen 3D-Zellen zu zuordnen. Hierfür berechnet eine Hashfunktion anhand der Punktkoordinaten der Ecken je einen Hashindex für die 3D-Zelle und legt sie in einer Hashtabelle ab. Danach werden die achsenparallelen Hüllquader der Tetraeder mit den 3D-Zellen geschnitten und mit den darin enthaltenen Ecken auf Kollision getestet.

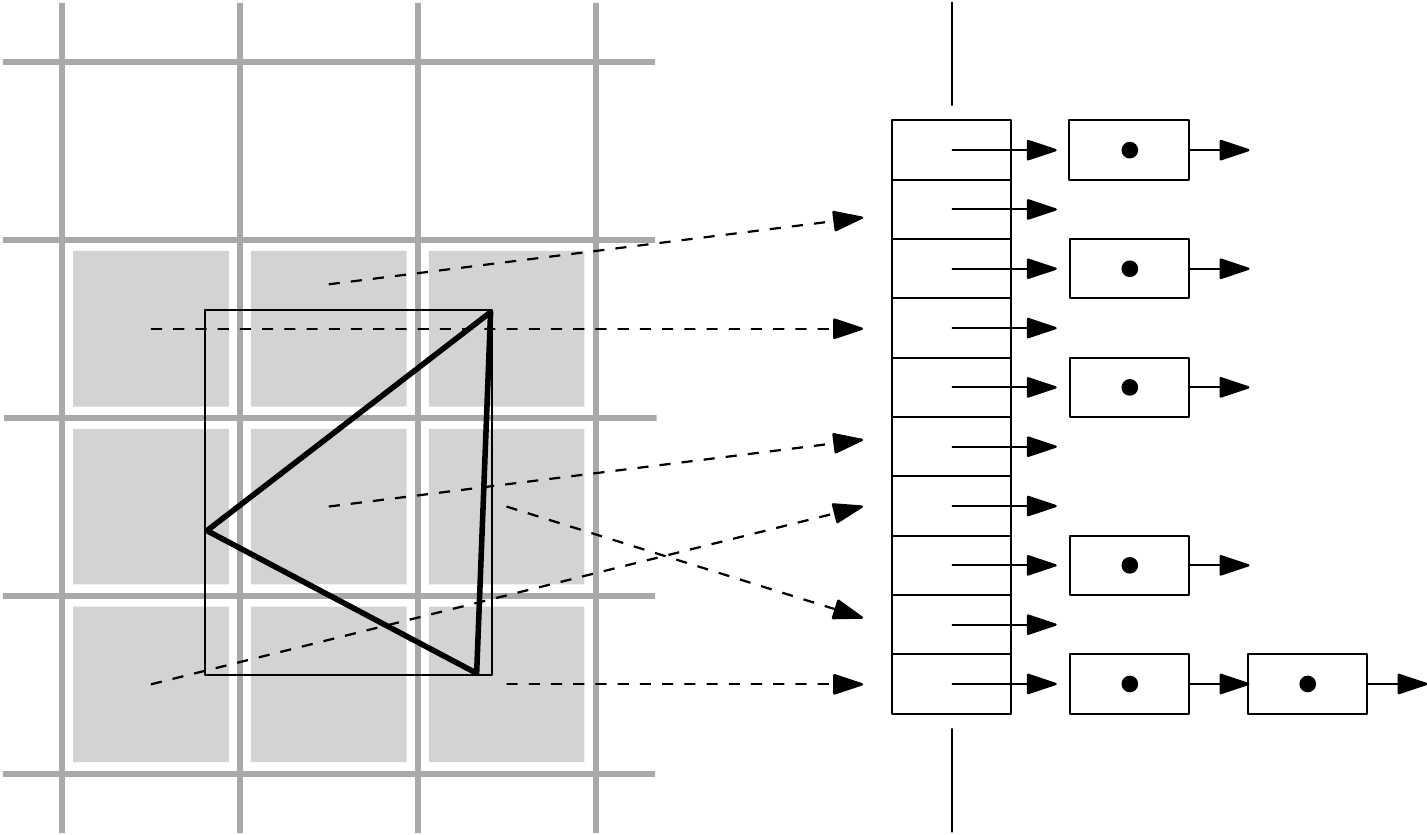
Alle Eckenpositionen werden zunächst mit Hilfe der Zellengröße l diskretisiert, danach werden ein Hashwert berechnet und die Ecke in die Listen der Hashtabelle eingefügt.	Der Hüllquader des Tetraeders schneidet die zu testenden 3D-Zellen. Zuerst wird der Hüllquader auf Kollision mit den Ecken in diesen 3D-Zellen geprüft und anschließend der Tetraeder.

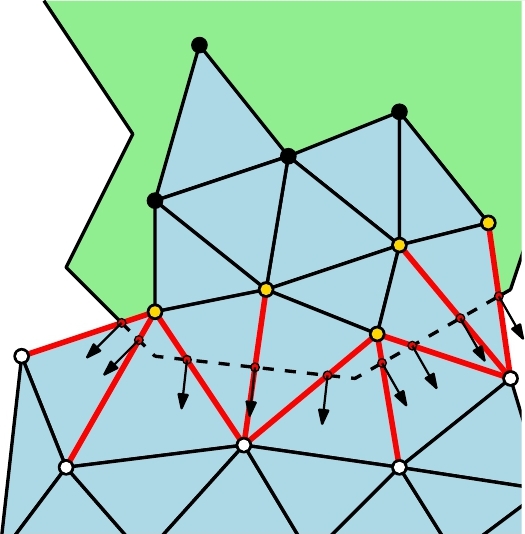
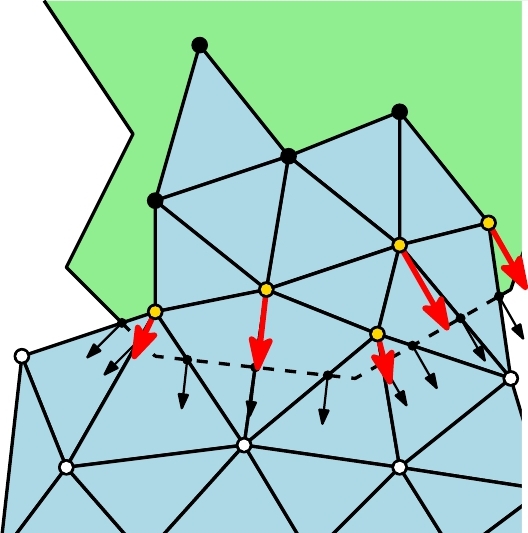
Ein wesentlicher Bestandteil der Kollisionserkennung sind die Kollisionsinformationen, die während der Kollisionserkennung berechnet werden. Hierzu werden alle kollidierenden Ecken in einem iterativen Prozess behandelt und jeweils eine approximierte Eindringrichtung berechnet. Mit dieser Eindringrichtung wird ein Eintrittspunkt an der Oberfläche berechnet, der für die Kollisionsauflösung verwendet wird.
Die Kollisionsauflösung unterteilt sich in zwei Schritte. Im ersten Schritt wird die Kollision aufgelöst indem Impulse berechnet werden, die die Ecke aus dem anderen Körper heraus korrigiert. Im zweiten Schritt wird die Haft- oder Gleitreibung zwischen den zwei Körpern in den Kollisionspunkten berechnet und ein entsprechender Impuls angewendet.

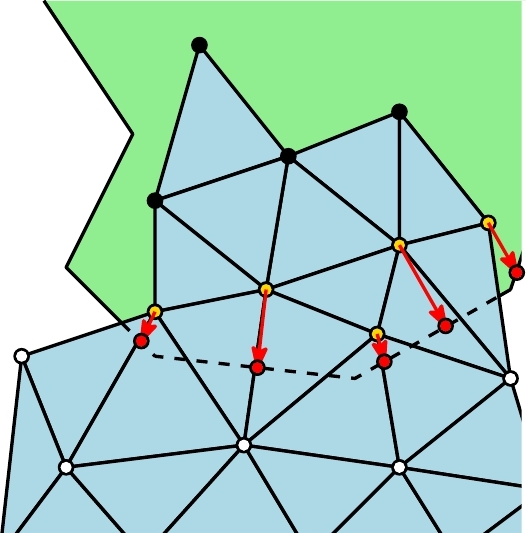Kollidierende Ecken mit angrenzenden nicht-kollidierenden Ecken besitzen Schnittkanten mit der Oberfläche.	Die Eindringrichtung berechnet sich durch eine gewichtete Mittelung der Oberflächennormalen.	Die approximierte Eindringrichtung wird mit der Oberfläche geschnitten, um den Eintrittspunkt zu erhalten.

Durch die Einführung mehrerer Hashtabellen bzw. einer Hashtabelle für jeden deformierbaren Körper konnte eine individuelle Optimierung für jeden Körper erreicht werden. Da verschiedene Körper unterschiedliche Tetraedernetzausprägungen besitzen können, wurde so erreicht, dass die Kantenlänge der 3D-Zellen optimal auf den jeweiligen Körper abgestimmt wird. Dies führte zu einem ausgewogenen Verhältnis zwischen der Anzahl der abgespeicherten Ecken in einer 3D-Zelle und der Anzahl überspannender 3D-Zellen des Hüllquaders eines Tetraeders. Des Weiteren wurden die Tetraeder, die sich nicht im Schnitt der Hüllquader der zwei kollidierenden Körper befinden, in der Kollisionsbehandlung ausgeschlossen. Diese beiden Vorgehen erbrachten eine Reduktion der Anzahl  der auf Kollision zu prüfenden Primitive und somit einer Verminderung der benötigten Rechenzeit. Eine deutliche Geschwindigkeitssteigerung war jedoch nur in komplexen Szenen zu beobachten, wohingegen in Szenen mit z.B. nur einem deformierbaren Körper meist nur eine kleine Verbesserung der benötigten Rechenzeit für die Kollisionserkennung pro Zeitschritt feststellbar war.

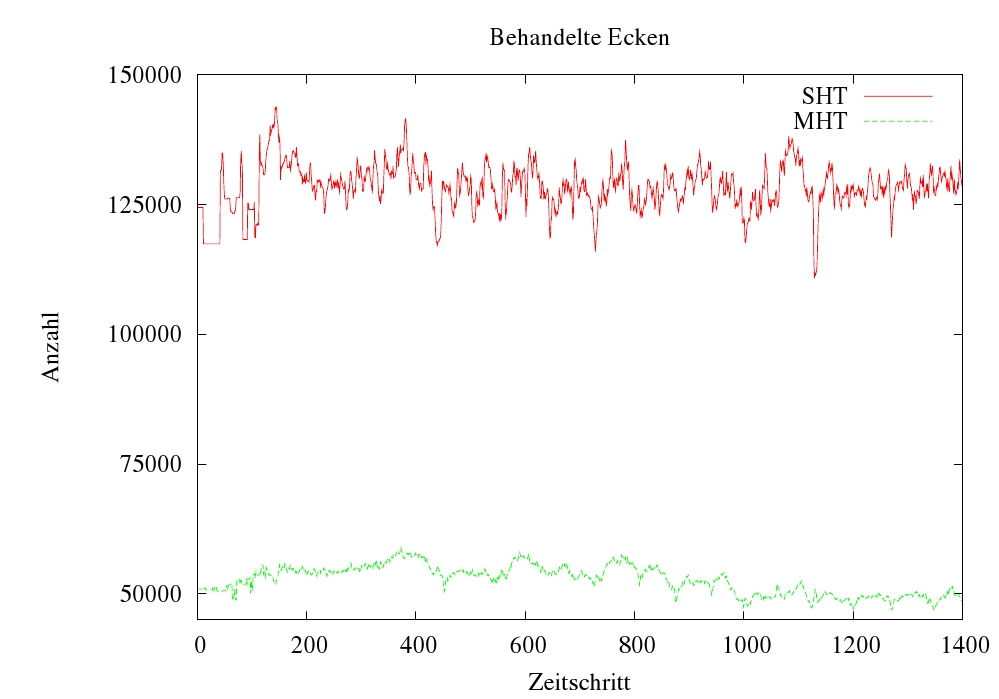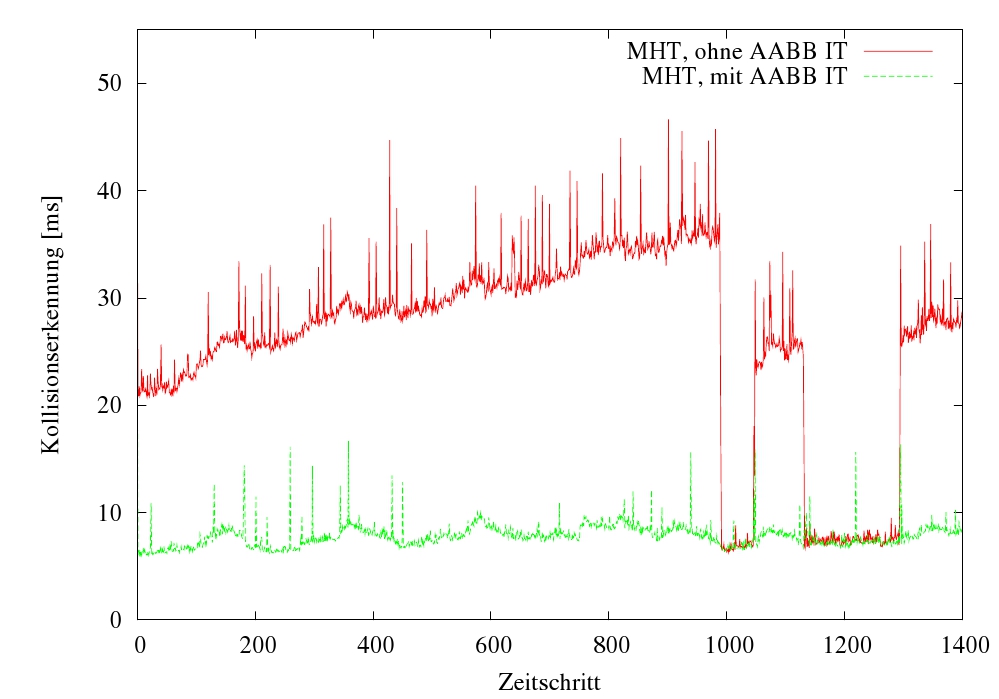Durch die Verwendung mehrerer Hashtabellen (MHT) konnte die Anzahl der zu behandelten Ecken im Gegensatz zur Verwendung einer einzigen Hashtabelle (SHT) stark reduziert werden.	Durch eine weitere Eingrenzung des Kollisionsraums mit Hilfe des Hüllquaderschnitttests (AABB IT) konnte die benötigte Rechenzeit der Kollisionserkennung in komplexen Szenen bedeutend verringert werden.

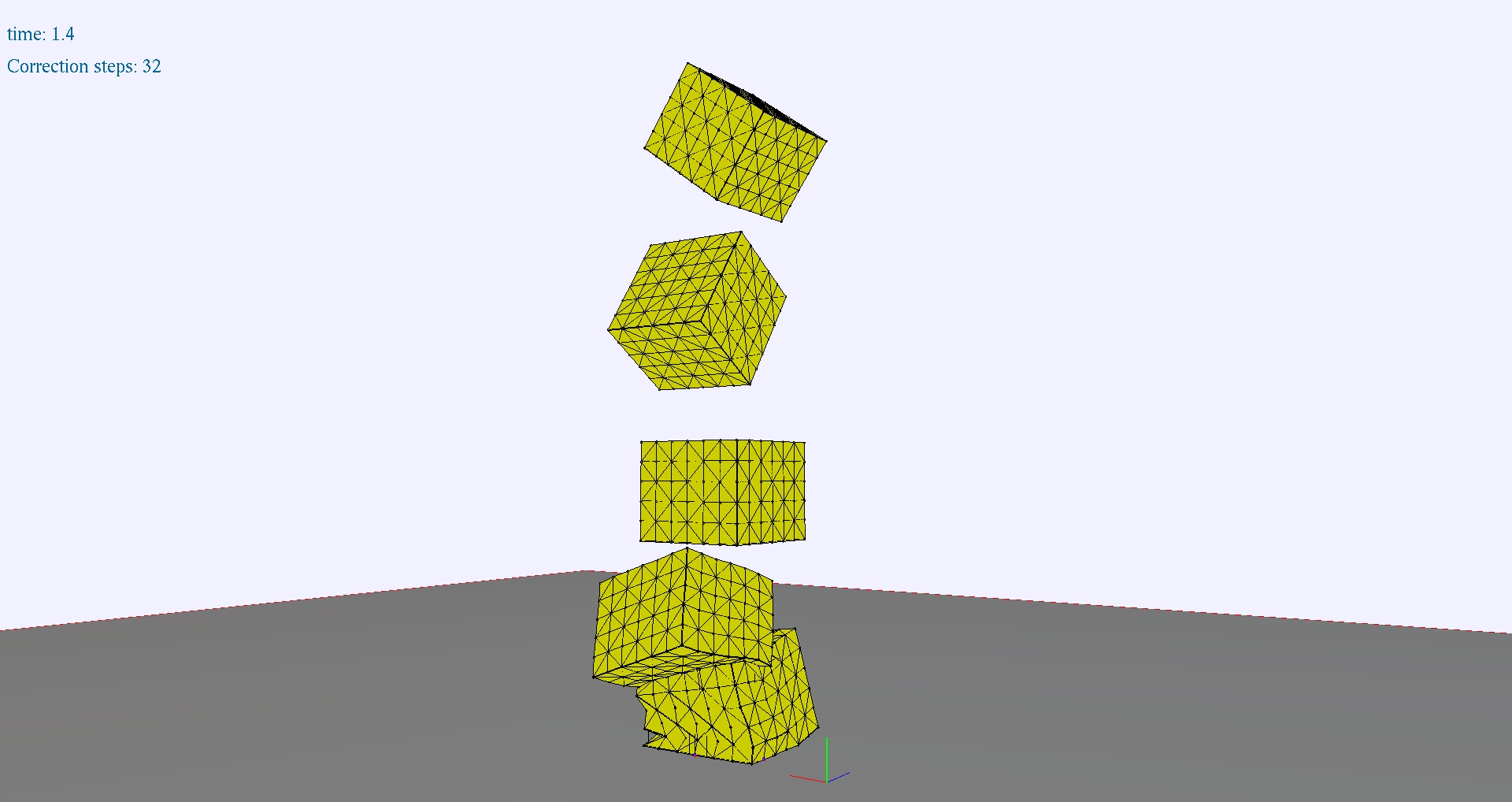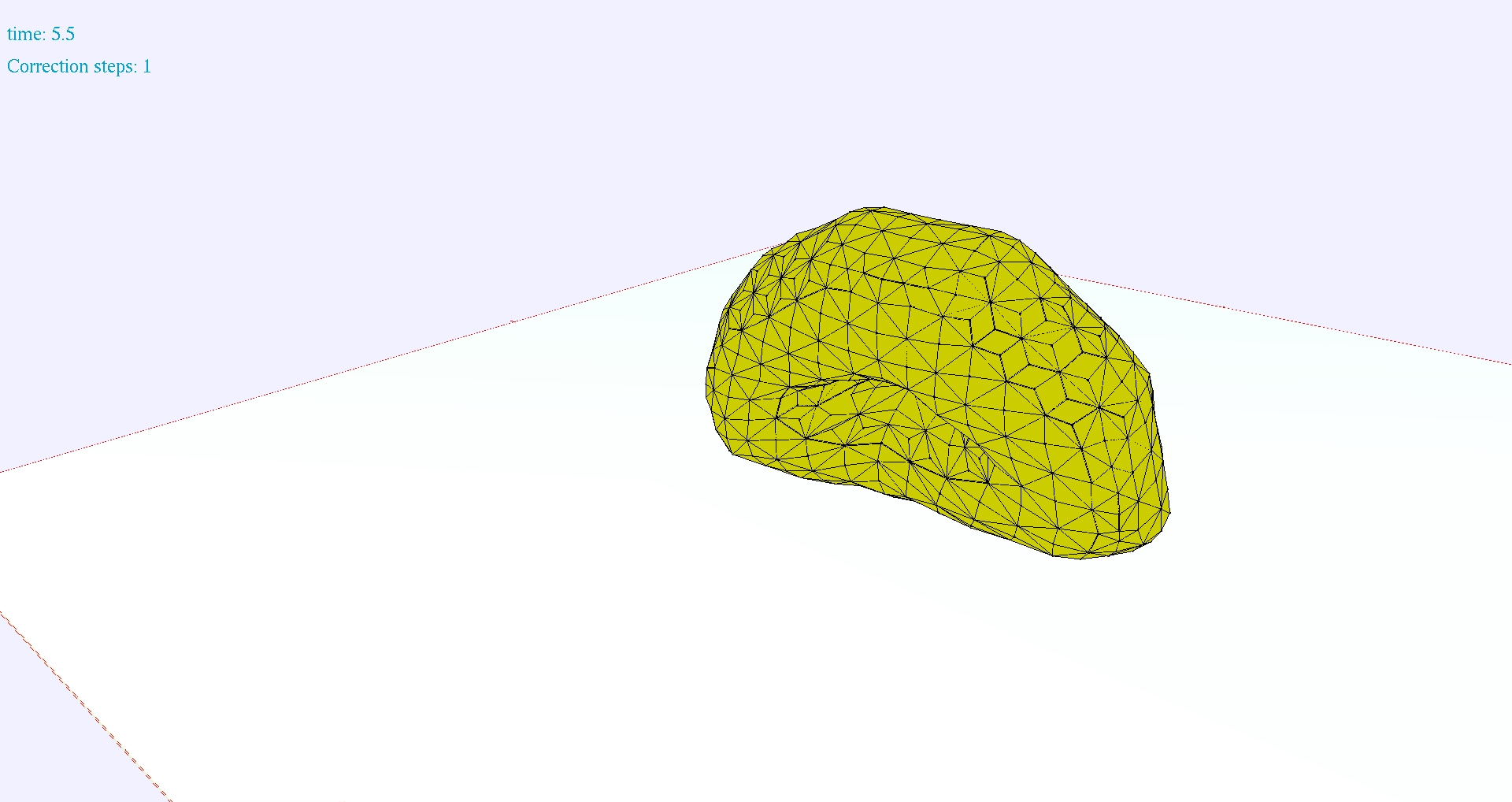Die oberen zwei Bilder zeigen je fünf aufeinander fallende deformierbare Würfel, die auf einen nicht nachgebenden Boden fallen. Die unteren zwei Bilder zeigen einen deformierbaren Torus, der ebenfalls auf einen nicht nachgebenden Boden fällt.

[1] M. Teschner, B. Heidelberger, M. Mueller, D. Pomeranets, M. Gross, Optimized Spatial Hashing for Collision Detection of Deformable Objects, Proc. Vision, Modeling, Visualization VMV ’03, Munich, Germany, pp. 47-54, Nov. 19-21, 2003.
[2] B. Heidelberger, M. Teschner, R. Keiser, M. Mueller, M. Gross, Consistent Penetration Depth Estimation for Deformable Collision Response, Proc. Vision, Modeling, Visualization VMV ’04, Stanford, USA, pp. 339-346, Nov. 16-18, 2004.