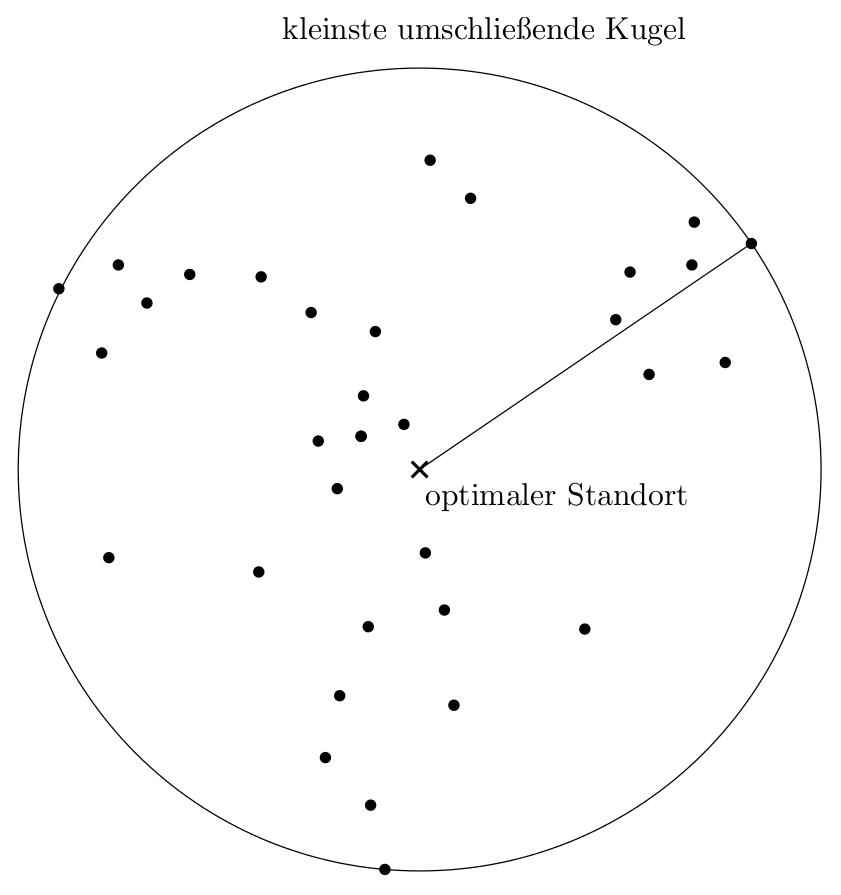
Das Problem, die kleinste umschließende Kugel einer Punktemenge zu finden, ist in zahlreichen Anwendungsgebiten von Bedeutung. Beispielsweise bei der Planung der Lage einer Notfall-Einrichtung, wie eines Krankenhaus, so dass der Abstand zwischen dem Krankenhaus und der entferntesten Wohnsiedlung minimal ist. Aber auch bei der Mustererkennung und in der Computergrafik beim Raytracing, Culling und der Kollisionserkennung kann das Problem auftreten.

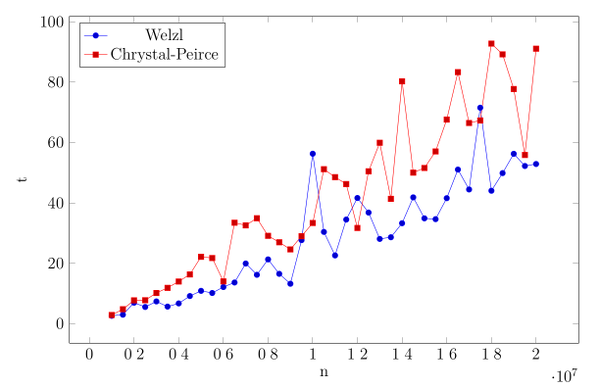
Es werden verschiedene Algorithmen zur Lösung des Problems vorgestellt und untersucht. Die vorgestellten Algorithmen sind: Ein randomisierter Algorithmus von Welzl mit Erweiterungen von Gärtner, eine geometrische Lösungen von Chrystal und Peirce aus dem 19. Jahrhundert, sowie ein Algorithmus von Elzinga und Hearn, wie auch von Friedman. Weiter wird die Formulierung des Problems als konvexes Optimierungsproblem und insbesondere als Quadratisches Programm betrachtet und dessen Lösung mit einem Active-Set Verfahren sowie dem Simplex-Algorithmus von Danzig beschrieben.

Abschließend wurden die Laufzeit ausgewählter Algorithmen für zufällig generierte Punktemengen gemessen und miteinander verglichen.