Bemerkung
Der genaue Termin wird noch später mit den Teilnehmern vereinbart.

Voraussetzungen Empfehlungen:
Programmierkenntnisse in z.B. C++ oder Python sind hilfreich.

Lehrinhalt:
Einführung in die Modellierung, Analyse, Rekonstruktion und Simulation geometrischer Daten (MARS-Geometrie :-) anhand praktischer Beispiele.

In diesem Praktikum werden klassische Techniken des Kurven- und Flächenentwurfs behandelt, die in zahlreichen CAD-Systemen Anwendung finden. Anhand kleiner Beispielprobleme können Sie sich den Stoff aus den Vorlesungen im Bereich der geometrischen Datenverarbeitung erarbeiten. Im Rahmen des Praktikums wird mit einer Python-Klassenbibliothek gearbeitet, die um Methoden und Klassen erweitert werden soll.

Vorkenntnisse aus den Vorlesungen Kurven und Flächen im CAD oder Rationale Splines oder vergleichbaren Veranstaltungen sind wünschenswert, aber nicht unbedingt erforderlich. Ein Teil der Inhalte des Praktikums ist auch in unseren CAGD-Applets , einem "interaktiven Tutorial zum geometrischen Modellieren", enthalten.

• Kurven
  • Interpolation mit kubischen B-Splines
    Dieser Versuch liefert einen Einstieg in die B-Spline-Theorie, die ein sehr mächtiges Instrument bei der Gestaltung gekrümmter Kurven und Flächen darstellt. Durch vorgegebene Punkte, beispielsweise Messdaten, soll ein natürlicher Spline gelegt und mit Hilfe des de Boor-Algorithmus ausgewertet werden.
  • Periodische Spline-Interpolation
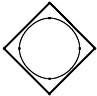
    Zur Interpolation und Approximation geschlossener Kurven sind sogenannte periodische Splines erforderlich. Damit sollen u. a. Kreise approximiert werden.
  • Parallelkurven
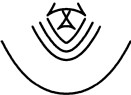
    In dieser Aufgabe sollen Parallelkurven von integralen Splines, wie sie beispielsweise bei der Mustererstellung oder Bestimmung von Fräsbahnen auftreten, mittels obiger Interpolationsverfahren approximiert werden, indem z. B. exakt bestimmte Punkte der Parallelkurve interpoliert werden. Abhängig von einer Fehlertoleranz müssen gegebenenfalls einzelne Spline-Segmente unterteilt werden.
• Flächen
  • Rotations- und Tensorproduktflächen
    Tensorproduktflächen entstehen durch Bewegen und Variieren einer Kurve im Raum. So ergibt sich durch Verschieben einer Kurve eine sogenannte Schiebfläche, durch Rotation einer Meridiankurve eine Rotationsfläche. Sie soll durch eine integrale Tensorproduktfläche approximiert werden. Mit Hilfe des Visualisierungsprogramms geomview kann die Fläche dargestellt werden.
  • Krümmungsvisualisierung
  • Interaktive Modellierung
    In diesem Versuch werden unterschiedliche Algorithmen für Dreiecksnetze implementiert.

Ablauf:
Die insgesamt 6 Versuche werden jeweils in einer alle 14 Tage stattfindenden Vorbesprechung vorgestellt. Die Versuche werden in Gruppen zu je zwei Teilnehmern durchgeführt. Jeder Versuch muss spätestens 4 Wochen nach der jeweiligen Vorbesprechung abgegeben werden.

Dateien:

• Geomview
• CAGD
• DrawFormat
• Algebra3
• Klassendiagramm

Anmeldung : yijun.xu@kit.edu

Bitte geben Sie folgendes an:

• MARS-Basispraktikum
• Name
• Matrikelnummer
• Prüfungsordnung (SPO 2008 / SPO 2015)