Objektrekonstruktion aus mehreren Tiefenbildern
- Typ:Diplomarbeit
- Datum:2001
- Autor(en):Bertrand Klimmek
- Links:.PDF
.BIB -
Das Reverse Engineering dreidimensional abgetasteter physischer Objekte hält eine Vielzahl von Problemen bereit. Eine Hauptschwierigkeit besteht bereits darin, verschiedene Datensätze, aus denen die vollständige Objektoberfläche rekonstruiert werden soll, in einem Datensatz zu integrieren (Registration). Dazu müssen die Koordinatensysteme der jeweiligen Teilansichten gegeneinander justiert werden.
Diese Arbeit verfolgt den Ansatz, zunächst geometrisch invariante Strukturelemente wie Kanten oder Ecken in sich überschneidenden Gebieten beider Dreiecksnetze auszumachen, um sie dann mitsamt Adjazenzen bzw. Inzidenzen als Teilgraphen einander zuzuordnen. Daraufhin wird eine Bewegung ermittelt, die die korrespondierenden Strukturelemente bestmöglich in Deckung bringt. Diese Bewegung wird auf das gesamte Dreiecksnetz angewendet, bevor schließlich ein iteratives Verfahren die Feinjustierung besorgt:
-
Krümmungsanalyse
Die Tiefenbilder liegen als Dreiecksnetze vor
Die differentialgeometrische Analyse besteht im wesentlichen aus einer quadratischen Approximation der Oberfläche: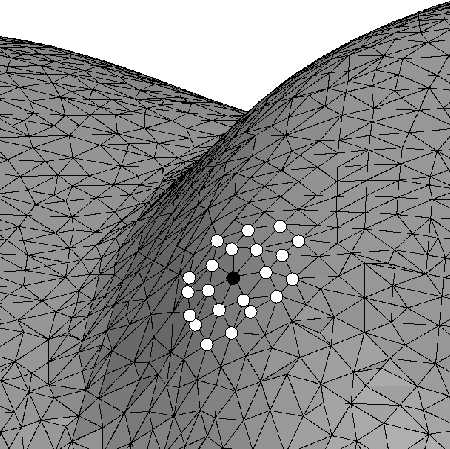
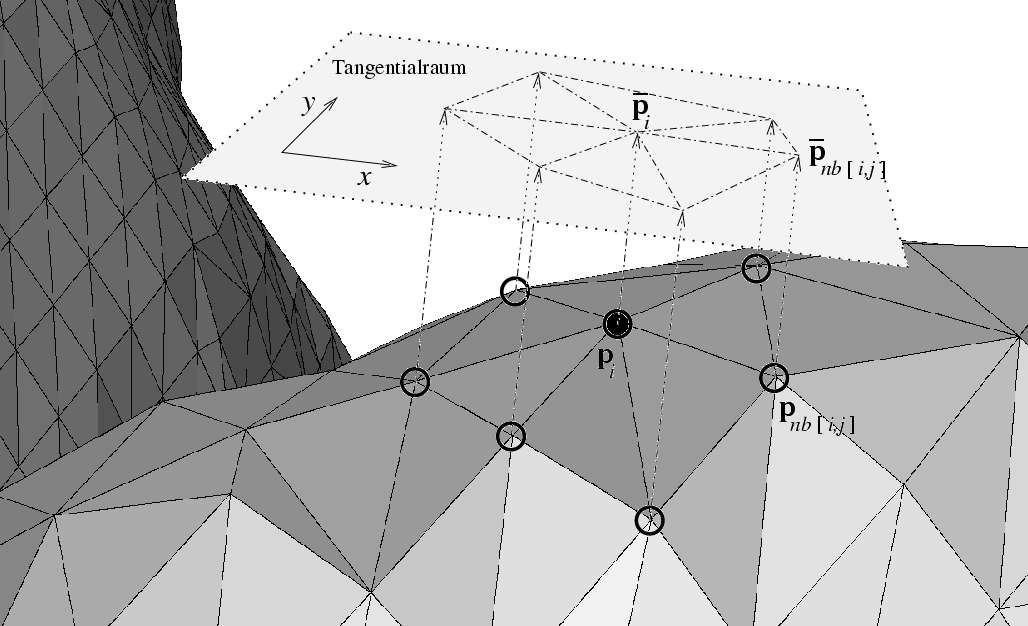
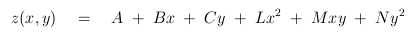
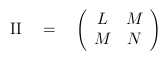
Die Hauptkrümmungen werden aus der zweiten Fundamentalform II gewonnen:
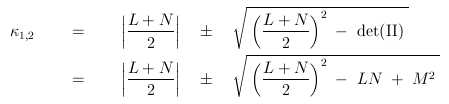
Ergebnisse der Krümmungsanalyse nach Vergleich mit Quantil-definiertem Schwellwert: krümmungsträchtige Gebiete sind markiert.
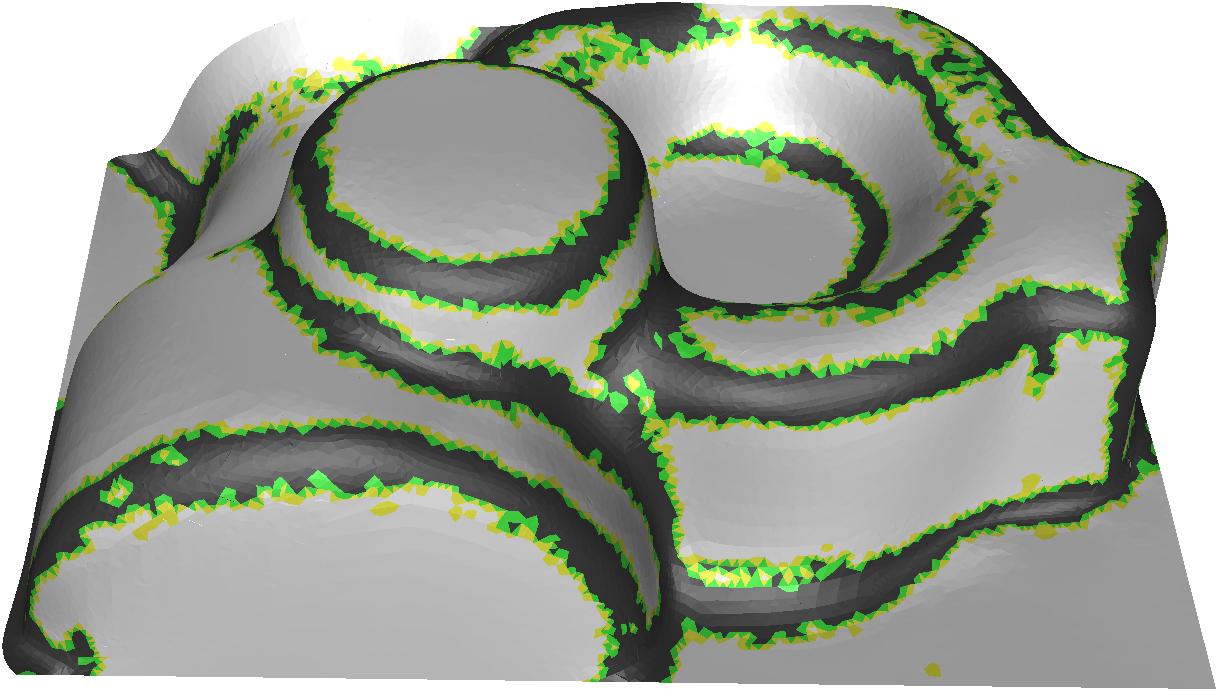
-
Skelettierung der Krümmungsgebiete
Die krümmungsträchtigen Gürtel werden auf wohldefinierte Kantenzüge ausgedünnt.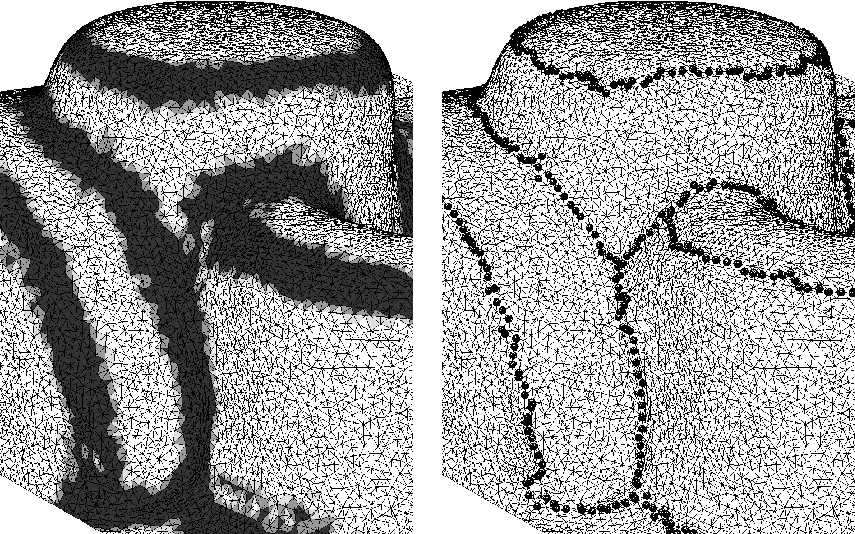
Durch die Kantenzüge mitsamt Verzweigungen entsteht eine Skelettstruktur und Flächenparzellierung.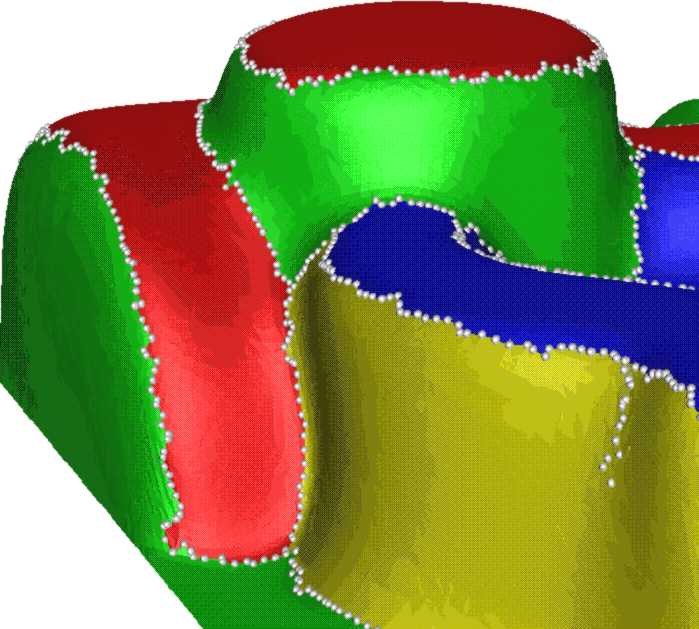
Der Metagraph als abstrakte Repräsentation des Skeletts mit Punkten (P), Aststücken (A) und Flächenstücken (F)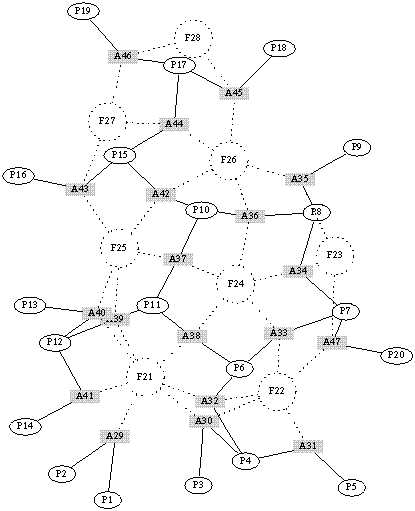
-
Gegenseitige Zuordnung
Paarweise werden Skelette von sich überschneidenden Objektansichten auf Teilgraphenisomorphie untersucht
Korrespondierende Strukturelemente S werden topologisch sowie anhand invarianter geometrischer Attribute ausgemacht und mit Hilfe von Zuordnungsfunktionen z festgehalten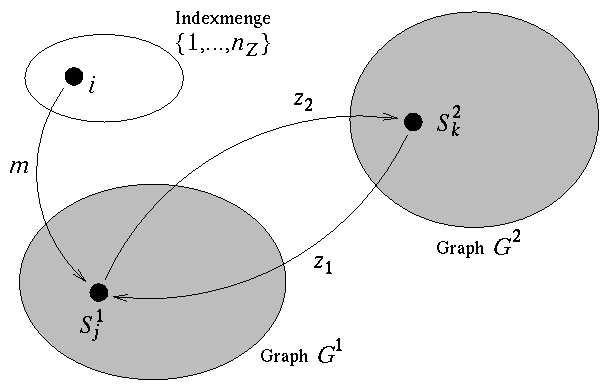
-
Bewegungsermittlung durch Quaternionenmethode
Ermittlung einer korrigierenden Relativbewegung T, die korrespondierende Strukturelemente bestmöglich in die Kongruenz überführt, durch Koordinatenvergleich (Kreuzkovarianz); zunächst werden die Schwerpunkte der Überschneidungsgebiete subtrahiert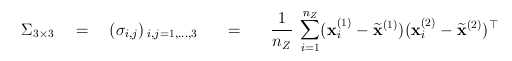
Die rotative Komponente der resultierenden Bewegung; jeder Punkt p wird um die Rotationsachse r gedreht. Darstellung bzgl. zweier verschiedener Basen: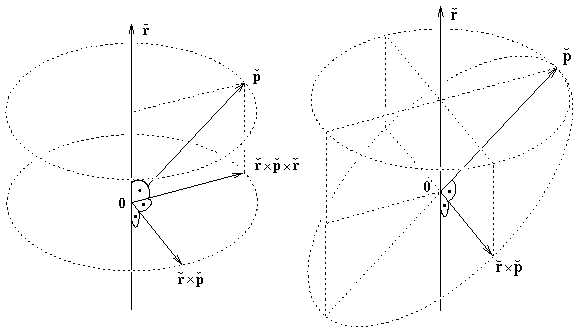
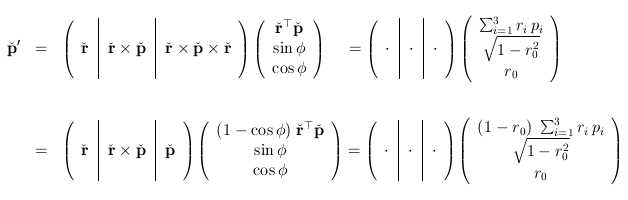
-
Feinjustierung
Ein iteriertes closest-point-Verfahren (ICP) ermittelt sukzessiv eine optimale korrigierende Bewegung
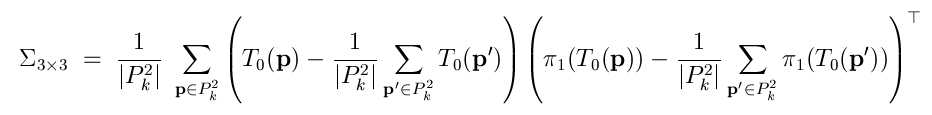
Die Bewegungsermittlung geschieht analog wie in der initialen Registration über die Kreuzkovarianz mittels Quaternionenmethode, operiert jedoch nicht mehr auf den extrahierten Strukturelementen, sondern wieder auf den Dreiecksnetzen
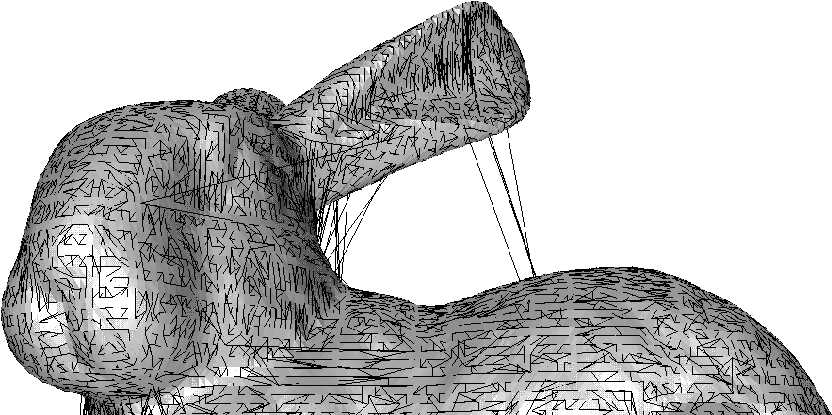
Die oct-tree-Struktur des zur Feinjustierung gegen Ende des Registrationsprozesses erforderlichen Suchbaums
