The Ball-Pivoting Algorithm – Eine Implementierung
- Typ:Studienarbeit
- Datum:2002
- Autor(en):Sven Oberländer
- Links:.PDF
.BIB -
Im Rahmen dieser Studienarbeit wurde der sogenannte "Ball-Pivoting Algorithm" (BPA) von Bernardini et al, der zur Rekonstruktion von Oberflächen aus Punktwolken mittels Dreiecksnetzen dient, implementiert und mit einem weiteren Algorithmus verglichen, dem Algorithmus von Linsen/Preuß. Hierzu wurde das Verhalten des Algorithmus genauer untersucht und Messungen zum Laufzeitverhalten und zur Korrektheit durchgeführt.
Schon in der Implementierungsphase stellte sich heraus, dass der BPA auf Grund seiner Konzeption bei bestimmten Punktkonstellationen Fehler verursacht. Solche Fehler können sowohl bei einem einzelnen Durchlauf als auch bei mehreren Durchläufen des BPA auftreten. Diese Fehler werden in der vorliegenden Implementierung abgefangen, ohne dass dies gravierende Auswirkungen auf die Laufzeit verursacht. Im Vergleich mit dem Algorithmus von Linsen/Preuß lieferte der BPA die qualitativ besseren Triangulationen, insbesondere neigte der BPA mit den vorgenommenen Ausbesserungen nur in Ausnahmefällen zu topologischen Fehlern in einer Triangulation. Bei der Messung der Laufzeit schnitt der BPA meist schlechter ab als der Algorithmus von Linsen/Preuß, war in Ausnahmefällen aber auch schneller.
Die Ergebnisse der durchgeführten Messungen zeigt die unten aufgeführte Tabelle. Als Testsystem wurde ein Rechner mit einem Intel Pentium II 400MHz Prozessor und 384MB Hauptspeicher unter der Linux-Distribution SuSE Linux 7.3 der SuSE Linux AG verwendet.
| Punktwolke | Linsen/Preuß-Algorithmus | ||||
|---|---|---|---|---|---|
| Dateiname | Anzahl Punkte |
verwendete Punkte |
gebildete Dreiecke |
gemessene Laufzeit |
Dreiecke/sec |
| bunny | 10.784 | 10.784 | 21.539 | 00:23,373 | 921.53 |
| club | 16.864 | 16.862 | 33.688 | 00:45,315 | 743,42 |
| fuss | 20.021 | 20.019 | 40.036 | 00:41,117 | 973,71 |
| knot | 10.000 | 10.000 | 20.001 | 00:27,827 | 718,76 |
| mannequin | 12.772 | 12.744 | 25.488 | 01:03,443 | 401,75 |
| monkey | 19.208 | 18.174 | 38.208 | 00:59,633 | 640,72 |
| nascar | 20.621 | 20.560 | 41.164 | 01:30,808 | 453,31 |
| oilpump | 30.937 | 30.936 | 61.794 | 00:51,101 | 1209,25 |
| skidoo | 37.974 | 37.869 | 75.843 | 01:00,827 | 1246,86 |
| teapot | 26.130 | 25.316 | 51.738 | 07:35,069 | 113,69 |
| Punktwolke | Ball-Pivoting Algorithm | ||||
| Dateiname | Anzahl Punkte |
verwendete Punkte |
gebildete Dreiecke |
gemessene Laufzeit |
Dreiecke/sec |
| bunny | 10.784 | 10.742 | 21.293 | 00:34,354 | 626,97 |
| club | 16.864 | 16.843 | 33.534 | 00:45,290 | 743,83 |
| fuss | 20.021 | 19.876 | 38.242 | 01:07,599 | 592,26 |
| knot | 10.000 | 9.966 | 16.929 | 00:35,386 | 565,22 |
| mannequin | 12.772 | 12.190 | 21.842 | 08:18,990 | 51,08 |
| monkey | 19.208 | 19.189 | 35.871 | 01:12,683 | 525,68 |
| nascar | 20.621 | 20.602 | 40.337 | 00:54,555 | 754,54 |
| oilpump | 30.937 | 30.098 | 58.800 | 01:50,215 | 560,67 |
| skidoo | 37.974 | 37.969 | 75.174 | 01:31,458 | 829,27 |
| teapot | 26.130 | 24.139 | 45.084 | 02:56,978 | 292,34 |
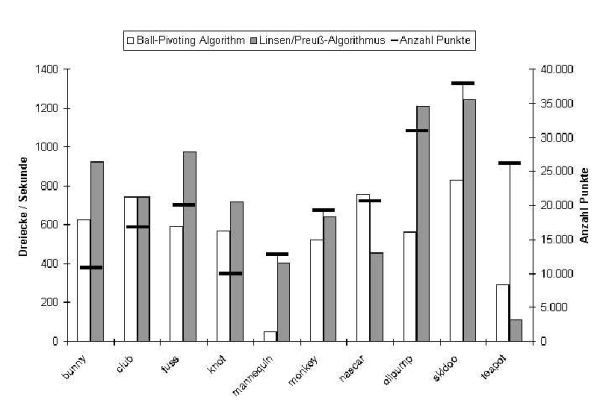
Hinweis: Die schwarzen Querstriche im Diagramm gehören zur Skala rechts und stehen für die Größe der Punktwolke.
Literatur
- [1] Fausto Bernardini, Joshua Mittleman, Holly Rushmeier, Cláudio Silva, Gabriel Taubin: The Ball-Pivoting Algorithm for Surface Reconstruction. IEEE Transactions on Visualization and Computer Graphics, Seite 349-359, IEEE Press, 1999
- [2] Lars Linsen: Oberflächenrepräsentation durch Punktwolken. Shaker Verlag Aachen, 2001
- [3] Stefan Preuß: Von Punktwolken zu Dreiecksnetzen. Diplomarbeit, Uni Karlsruhe, 2002
