Die Krümmung ist eine der wichtigsten geometrischen Eigenschaften einer Fläche. Sie ist in der Computergrafik und der geometrischen Modellierung von großer Bedeutung. Die Krümmungsinformation kann zum Beispiel zur Segmentierung, Flächenklassifikation, Flächenrekonstruktion und -registrierung benutzt werden. Eine Punktwolke ist eine Menge von Punkten, die auf der Oberfläche eines Objektes liegen. Die Punkte können zum Beispiel durch einen 3D-Scanner abgetastet werden. Durch eine Punktwolke kann die Oberfläche eines realen Objekts mit Hilfe von Computern dargestellt werden.

Diese Arbeit beschäftigt sich mit der Berechnung und Visualisierung der Krümmungsinformation auf einer Fläche, die durch eine Punktwolke gegeben ist. Das Ziel dieser Arbeit besteht darin, zuerst die Krümmungswerte jedes Punktes auf einer Punktwolke möglichst genau zu berechnen, danach die Oberfläche eines Objekts durch Krümmungswerte farbig darzustellen und zusätzlich die Krümmungslinien zu vorgegebenen Punkten auf der Oberfläche zu zeigen.

Zunächst wurden theoretische Grundlagen und verschiedene Methoden zur Krümmungsberechnung vorgestellt. Danach wurden sieben Methoden - auf verschiedenen analytischen Flächen, auf verrauschten analytischen Flächen und auf von Scannern abgetasteten Flächen - implementiert und getestet. Die Arbeit endet mit einer Analyse und einem Vergleich der Testergebnisse.

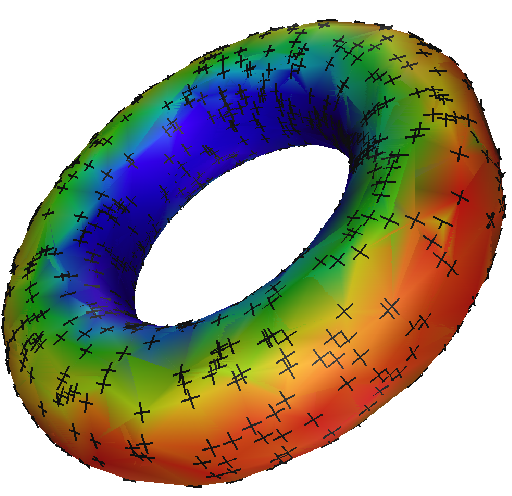
Visualisierung der Gauß-Krümmungen und Krümmungsrichtungen auf einem Torus		Zwei Krümmungslinien unter Berücksichtigung  der Geschlossenheit auf der Oberfläche einer Banane

Die Ergebnisse zeigen:       

1. Die Approximation durch ein allgemeines biquadratisches Patch, wahlweise in Verbindung mit der gewichteten Methode der kleinsten Quadrate, ist bei den verwendeten Beispielen am genauesten.
2. Die obigen Verfahren sind auch auf den verrauschten Flächen am genauesten.
3. Die optimale Anzahl der Nachbarn hängt eng vom Flächentyp, der Größe des Rauschens und der Punktdichte ab. Die optimale Anzahl der Nachbarn bei obigen Verfahren liegt zwischen 8 und 25.

Wegen der Schwierigkeit der Auswahl eines passenden Verfahrens und einer optimalen Anzahl von Nachbarn ist es sinnvoll, eine Bewertungsmethode zu entwickeln, die die Zuverlässigkeit einer Methode zur Krümmungsberechnung schätzt, und die Ergebnisse von verschiedenen Methoden zu vergleichen. In dieser Arbeit wurden zwei Bewertungsmethoden vorgestellt. Die Testergebnisse zeigen, dass diese Bewertungsmethoden nicht immer sinnvoll sind.

Weitere Verbesserungsmöglichkeiten bestehen darin, dass wir

1. bessere Bewertungsmethoden suchen,
2. eine variable Anzahl von Nachbarn für verschiedene Punkte der Punktwolke betrachten und
3. andere Gewichtsfunktionen bei MLS-Methoden (Moving-Least-Squares-Methoden) verwenden, da die MLS-Methoden die unregelmäßige Verteilung der Punkte einer Punktwolke berücksichtigen.