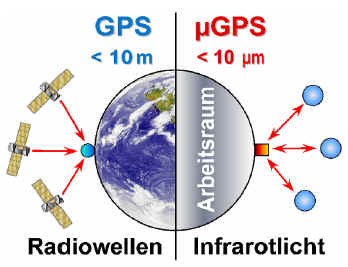
Diese Arbeit beschäftigt sich mit mit einer Reihe Methoden zur Kalibrierung des optischen Positionsmeßsystems µ-GPS. Wie der Name µ-GPS bereits impliziert, handelt es sich hierbei um ein System das analog zum ’Global Positioning System‘ mehrere Längen zu Referenzobjekten misst und daraus eine Position berechnet. Während das satellitengestützte GPS allerdings  über die Messung von Signallaufzeiten und deren Synchronisation arbeitet, basiert das µ-GPS auf einem optisch-interferometrischen Ansatz und besitzt eine Größenordung im Bereich von Zentimetern bis wenigen Metern, erreicht aber eine Genauigkeit im Micrometerbereich. Aufgrund einiger Fertigungsungenauigkeiten in optischen Komponenten wie Linsen und Reflektoren sind die vom System gemessenen Längen fehlerbehaftet. Der hier vorgestellte Ansatz ermöglicht es mittels eines geeigneten Kalibrier- und Interpolationsverfahrens die Genauigkeit des Mess-Systems erheblich zu verbessern.

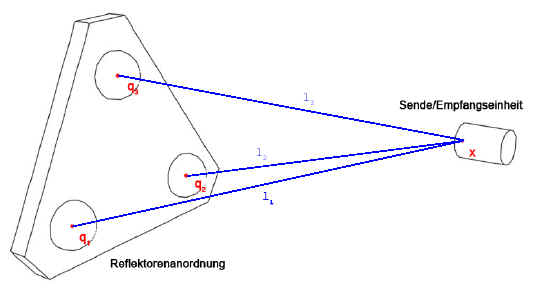
Dieser Ansatz greift auf Methoden der Spline Interpolation und Verfahren der numerischen linearen Algebra zurück und ist im Stande unter Echtzeitbedingungen zu funktionieren. Dabei modelliert eine mittels Tensorprodukt-Splines realisierte Fehlerfunktion den entstehenden Messfehler. Weiterhin werden Methoden vorgestellt, die die Probleme bei der Berechnung der Fehlerfunktion, welche sich aus praktischen Rahmenbedinungen ergeben, behandeln.

Anhand der Verbesserungen durch die vorgestellte inverse Tensorproduktspline-Interpolation wurden ernome Genauigkeitssteigerungen erreicht, sodass das System jetzt im Stande ist Positionen mit einer Genauigkeit von 5-7 µm zu messen. Darüberhinaus erlauben es die Verbesserungen einen größeren Arbeitsraum auszunutzen, da sich jetzt auch in den Randbereichen des Messvolumens der Fehler innerhalb der gewünschten Genauigkeitsgrenzen bewegt.

Diese Studienarbeit ist in Zusammenarbeit mit dem Institut für Angewandte und Numerische Mathematik der Universität Karlsruhe entstanden.