Am Institut für Betriebs- und Dialogsysteme wird ein 3D-Scanner entwickelt, welcher – aus Aufnahmen eines mit strukturiertem Licht beleuchteten Objekts – Punkte auf der Objektoberfläche berechnet. Der kostengünstige Scanner besteht aus einer digitalen Kamera und einem Projektor, der üblicherweise für Präsentationen eingesetzt wird. Erschwingliche Optiken für Kamera und Projektor lassen sich nur näherungsweise mit dem Lochkameramodell beschreiben, da diese zu Verzerrungen führen, die die Genauigkeit des Scanners wesentlich verschlechtern. Die Aufgabe dieser Diplomarbeit bestand darin, ein robustes Linsenentzerrungsverfahren zu entwickeln, welches alleine anhand von Aufnahmen gerader Kanten die Parameter für die radiale und tangentiale Linsenverzerrung bestimmt.

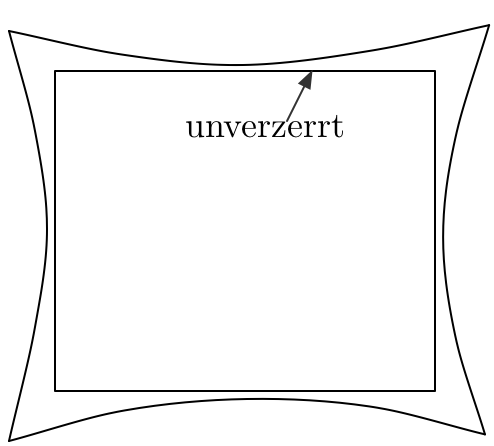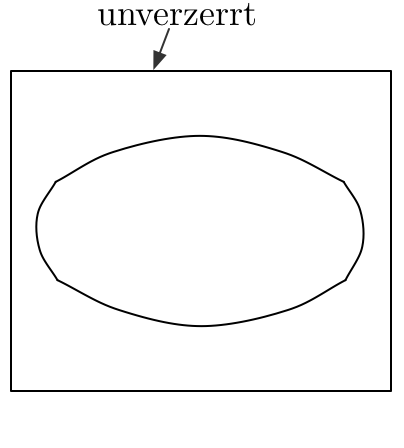
Tonnenförmige Verzerrung.	Kissenförmige Verzerrung.

In dieser Arbeit werden zwei verschiedene Methoden dargestellt. Eine ist eine robuste halbautomatische Methode zur Korrektur der radialen Linsenverzerrung in Bildern [1]. Sie basiert auf der Hough-Transformation und wird bei unbekannten Kameras, ohne Kalibierung, verwendet.

Insgesamt besteht die Methode aus zwei Schritten:

1. automatische oder halbautomatische Bestimmung der Kurven, die geradlinig sein sollen
2. iterative Veränderung des Verzerrungsparameters unter Maximierung der Geradlinigkeit der Kurven

Eine bekannte Methode, um die Geradlinigkeit von Kurven zu messen, ist die Hough-Transformation. Ein wichtiger Vorteil der Methode ist, dass sie einfach zu implementieren ist. Die Nachteile dieser Methode sind, dass sie viele Voraussetzungen und Beschränkungen hat: Sie kann nur die radialen Verzerrungsparameter bestimmen und der relevante Bildbereich (engl. region of interest, ROI), in dem eine Gerade gefunden werden soll, muss im ersten Schritt der Methode von Hand ausgewählt werden.

 

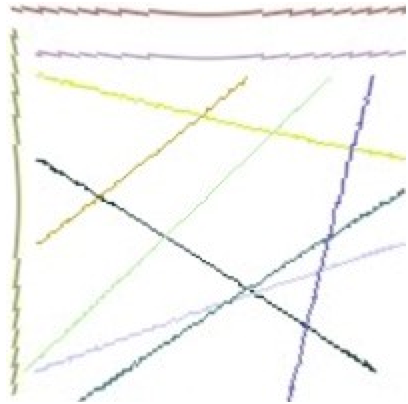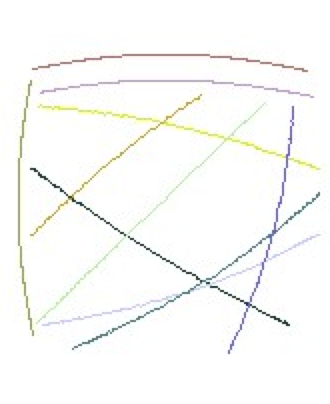
Ein künstlich verzerrtes Bild.	Auswählen des relevanten Bildbereichs.	Das entzerrte Bild.

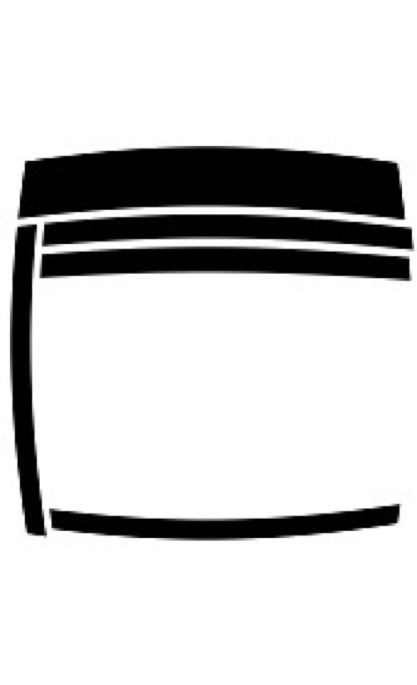
Um die Linsenverzerrungsparameter genauer und automatisch zu bestimmen, wurde eine andere robustere Linsenentzerrungsmethode implementiert [2]. Diese ist ein automatisches Verfahren, das auf dem robusten kleinsten quadrierten Median basiert. Es benutzt eine lineare Lösung als Startwert für das anschließende nichtlineare Optimierungsproblem. Bei diesem Verfahren wird zweimal der LMedS-(Least Median of Squares)-Algorithmus verwendet, einmal für das ganze Verfahren und einmal im zweiten Schritt dieses Verfahrens. Das Ziel des ersten Schritts ist, für jede verzerrte Kurve eine Reihenfolge der Kurvenpunkte zu erzeugen. Die Verzerrung des Bilds ist meistens kleiner als ein Pixel, deshalb werden hier Kantendetektionsalgorithmen mit Subpixelgenauigkeit verwendet. In dieser Arbeit wird eine Methode von Devernay [3] verwendet.

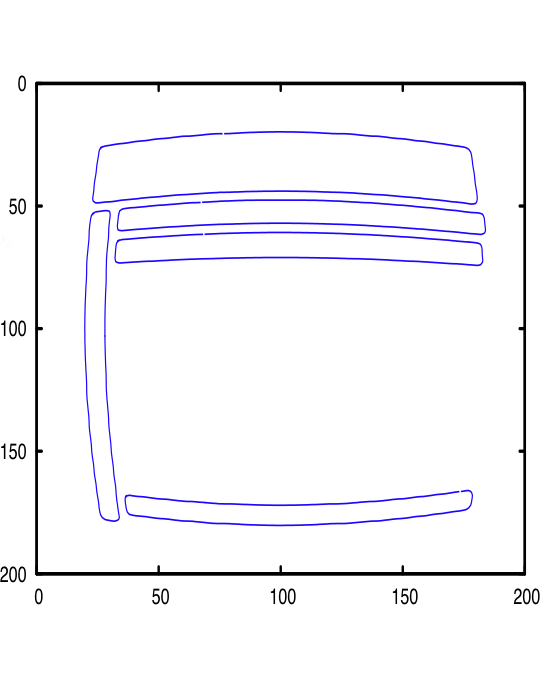Subpixelgenaue Kantendetektion.
Vergleich der pixelgenauen (rot) mit der subpixelgenauen (blau) Kantendetektion.

Im zweiten Schritt werden die Geradenparameter durch den LMedS-Algorithmus für jeden Kantenzug bestimmt. Nach der Bestimmung der Anzahl der Stichproben werden für jede Stichprobe die Mediane der Residuen-Quadrate bestimmt. Dann wird der minimale Median aller Stichproben berechnet, mit dem ein Schwellwert zur Bestimmung der Ausreißer bestimmt wird. Zum Schluss werden die Verzerrungsparameter nach dem Verwerfen der Ausreißer neu berechnet.

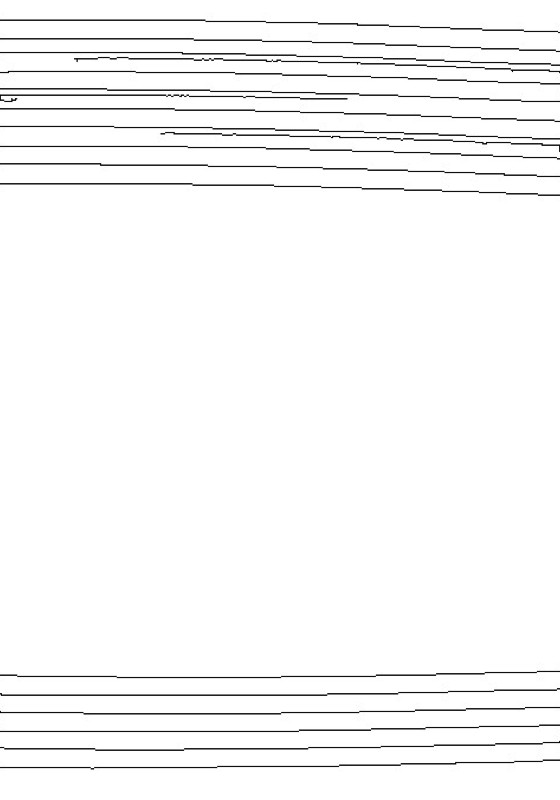
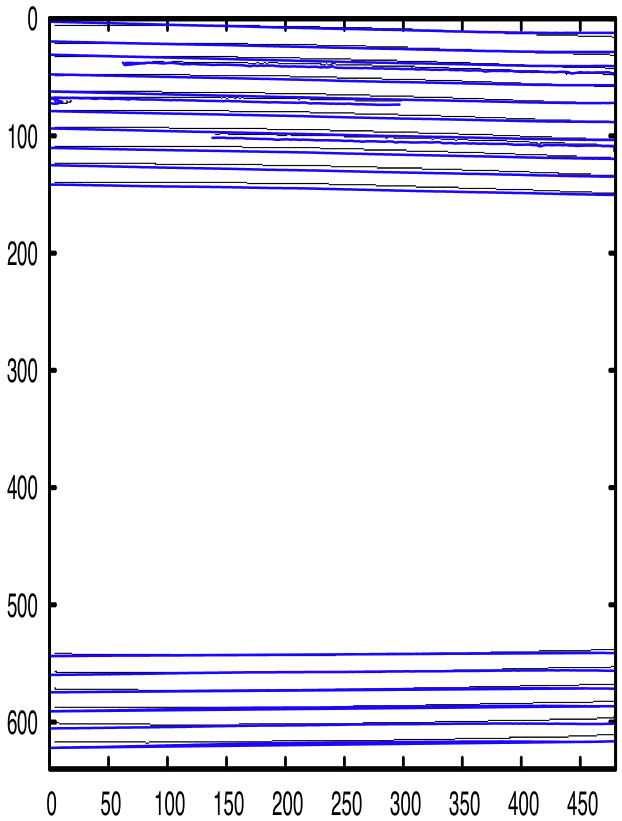
Ein Weitwinkelfoto einer Kompakt-Digitalkamera.	Kantendetektion mit Subpixelgenauigkeit.	Vergleich der entzerrten (blauen) und verzerrten (schwarzen) Kurven.	Das entzerrte Foto.

 

Ein Foto einer Handykamera.	Das entzerrte Foto.

 

Beide Linsenentzerrungsverfahren haben noch einige Probleme, die in zukünftigen Arbeiten gelöst werden können. Hier diskutieren wir nur die Probleme des zweiten Verfahrens. Die Ergebnisse der Tests mit künstlichen Daten zeigen, dass das nichtlineare Optimierungsverfahren eventuell nicht konvergiert, wenn die Koordinaten der Kantenpunkte nur pixelgenau sind. Das heißt, wenn dieses Verfahren mit realen Daten verwendet werden soll, dann muss die Kantendetektion sehr genau sein. Ein weiterer Schritt ist die Integration dieses Linsenentzerrungsverfahrens in die optische Triangulierung und damit in das Scansystem.

[1] Rita Cucchiara, Costantino Grana, Andrea Prati und Roberto Vezzani. A Hough transform-based method for radial lens distortion correction. In ICIAP ’03: Proceedings of the 12th International Conference on Image Analysis and Processing, S. 182-187, Washington, DC, USA, 2003. IEEE Computer Society.

[2] Moumen T. El-Melegy und Aly A. Farag. Nonmetric lens distortion calibration: Closed-form solutions, robust estimation and model selection. In ICCV ’03: Proceedings of the Ninth IEEE International Conference on Computer Vision, S. 554-559, Washington, DC, USA, 2003. IEEE Computer Society.

[3] Frédéric Devernay. A non-maxima suppression method for edge detection with sub-pixel accuracy. Technical Report RR-2724, Institut National de Recherche en Informatique et en Automatique (INRIA), November 1995