Übersicht
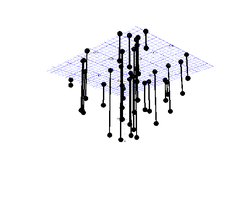
Ein häufiges Problem der Computergrafik ist die Bestimmung einer durch eine Punktwolke laufenden Funktion. Es tritt zum Beispiel auf bei einer möglichst genauen Rekonstruktion einer Oberfläche im Computer, von der mit einem Laserscanner eine Punktwolke erzeugt wurde.
Hier wird ein Algorithmus analysiert, der unter der Annahme, dass die Oberfläche stetig, konvex und differenzierbar war, versucht eine Oberfläche zu rekonstruieren, die selbige Bedingungen erfüllt. Statt auf allgemeinen Oberflächen, arbeitet er auf bivariaten Funktionen.
Dafür wird jeweils eine minimale und maximale Schranke für alle lösenden Funktionen gesucht. Die maximale Schranke ist die konvexe Hülle der Punkte. Hat man an jedem Punkt eine Normale der originalen Oberfläche gegeben und damit einen Halbraum in dem die originale Oberfläche liegt, so hat man die minimale Schranke als Rand des Schnittes all dieser Halbräume.
Aus diesen beiden Schranken versucht man sich iterativ einer Lösung zu nähern, indem man eine Funktion punktweise als gewichtete Summe des Minimums und Maximums definiert.
Hier wird ein Algorithmus analysiert, der unter der Annahme, dass die Oberfläche stetig, konvex und differenzierbar war, versucht eine Oberfläche zu rekonstruieren, die selbige Bedingungen erfüllt. Statt auf allgemeinen Oberflächen, arbeitet er auf bivariaten Funktionen.
Dafür wird jeweils eine minimale und maximale Schranke für alle lösenden Funktionen gesucht. Die maximale Schranke ist die konvexe Hülle der Punkte. Hat man an jedem Punkt eine Normale der originalen Oberfläche gegeben und damit einen Halbraum in dem die originale Oberfläche liegt, so hat man die minimale Schranke als Rand des Schnittes all dieser Halbräume.
Aus diesen beiden Schranken versucht man sich iterativ einer Lösung zu nähern, indem man eine Funktion punktweise als gewichtete Summe des Minimums und Maximums definiert.
 |
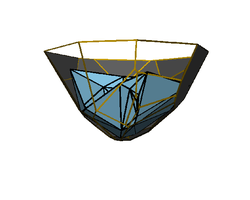 |
| Punktwolke | minimale und maximale Schranke |
 |
 |
 |
| nach der ersten Iteration | nach der zweiten Iteration | nach der dritten Iteration |
