Netzreduktion findet in vielen Bereichen Anwendungen. So trifft man sie vor allem da wieder, wo es darum geht, Netze in Echtzeit darzustellen. Neben der schnelleren Darstellbarkeit spielt auch der reduzierte Speicherbedarf eine Rolle. Die Motivation für diese Arbeit begründet sich aber in einem weiteren Aspekt: Die Reduzierung von Netzen, um sie handhabbarer für Aufgaben, wie die automatische Generierung von Bastelbögen, zu machen. Sowohl dem Ergebnis des Bastelbogenprogramms – ein planares, zusammenhängendes Netz mit selbständig angefügten Klebelaschen in angemessener Zeit zu generieren – als auch dem Benutzer, der aus dem planaren Netz wieder ein räumliches Objekt zusammenfügen soll, ist es zuträglich, die Komplexität der Aufgaben und somit der Anzahl der Knoten, Kanten und Facetten unter oben genannten Bedingungen soweit wie möglich zu reduzieren. Wir sind besonders daran interessiert, den Teil des Netzes zu reduzieren, in dem die Geometrie eine hohe Komplexität des Netzes nicht rechtfertigt. Betrachtet man das Bastelbogenprogramm, möchte man in Gebieten, in denen sich die Normalen der Facetten nur geringfügig ändern, die Facettenanzahl möglichst gering halten. Deswegen liegt ein Schwerpunkt dieser Arbeit im Zusammenfassen koplanarer und quasi koplanarer Facetten, das heißt im Zusammenfassen solcher Facetten, deren Normalen in dieselbe Richtung zeigen bzw. deren minimale Normalenhüllkegel einen kleinen Winkel einschließen.

Die Eingabe des Algorithmus besteht aus einem polygonialen Netz. Ausgegeben wird ein in Knoten, Kanten und Facetten reduziertes Netz. Der Vereinfachungsalgorithmus berechnet aus einer Menge zusammenhängender Facetten eine planare Facette. Diese zusammenhängende Facetten bezeichnet man als Superfacette. Die Superfacette wird zu einer einzigen Facette verschmolzen. Das Verschmelzen von, je nach Verfahren, zwei oder mehreren Facetten beeinflusst jedoch nur die Netztopologie, die Geometrie des Netzes bleibt (zunächst) erhalten. Anschließend wird das topologisch veränderte Netz zusätzlich in seiner Geometrie manipuliert. EIne planare Facette erhält man jetzt, indem man eine Ausgleichsebene aus allen Knoten der Superfacette berechnet und deren Randknoten auf die Ausgleichsebene projiziert.

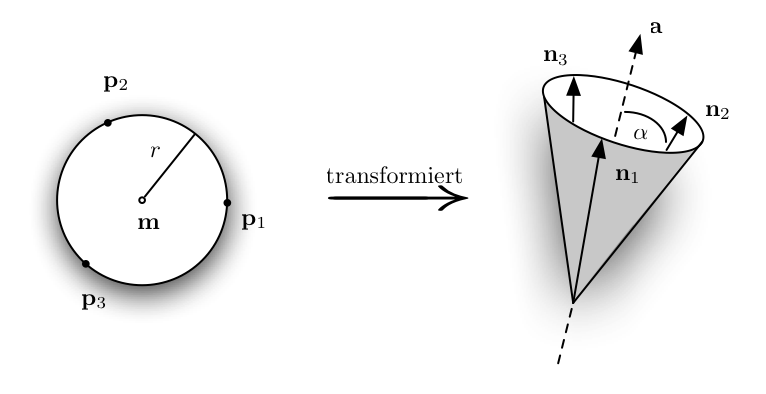
Ein flexibler Ansatz zur Berechnung der Superfacette bietet das Verfahren des minimalen Normalenhüllkegels. Dabei bestimmt man eine Startfacette und erweitert diese zu einem Gebiet zusammenhängender Facetten derart, so dass die zugehörigen Normalen einen minimalen Normalenhüllkegel bilden. Um diesen Kegel zu berechnen wird das duale Problem betrachtet, den kleinsten umschließenden Kreis einer Menge von Punkten in der Ebene zu berechnen. Hierzu verwenden wir eine Modifikation des Welzl-Algorithmus.

Die Implementierung des Vereinfachungsverfahrens liefert in der Praxis gute Resultate. Die Komplexität der Modelle konnte erheblich reduziert werden. Auch wurden bei entsprechender Wahl der Parameter die wesentlichen Merkmale des Netzes erhalten. Probleme gibt es beim Auftreten von Selbstberührungen. Ursache dafür ist die bei der Implementierung des Vereinfachungsalgorithmus zugrunde liegende Datenstruktur OpenMesh. Diese konnte anfangs überhaupt nicht, später nur bedingt mit Selbstberührungen umgehen. Da diese aber bei großen Netzen sehr häufig auftreten, wird das Gesamtresultat der Arbeit durch Selbstberührungen stark beeinträchtigt.

Ausbaufähig ist auch das Laufzeitverhalten der Methode zur Erzeugung der Superfacette durch den modifizierten Welzl-Algorithmus. Dieses verschlechtert sich erheblich, wenn die Anzahl der Facetten pro Region große Werte annimmt. Eine mögliche Lösung, die wahrscheinlich erheblich zur Laufzeitverbesserung beitragen würde, wäre eine iterative Berechnung des minimal umschließenden Normalenhüllkegels. Zur Verbesserung der Netzqualität wurde anschließend eine Optimierung durchgeführt, die möglichst planare Facetten und möglichst lineare Kantenzüge erzeugt.

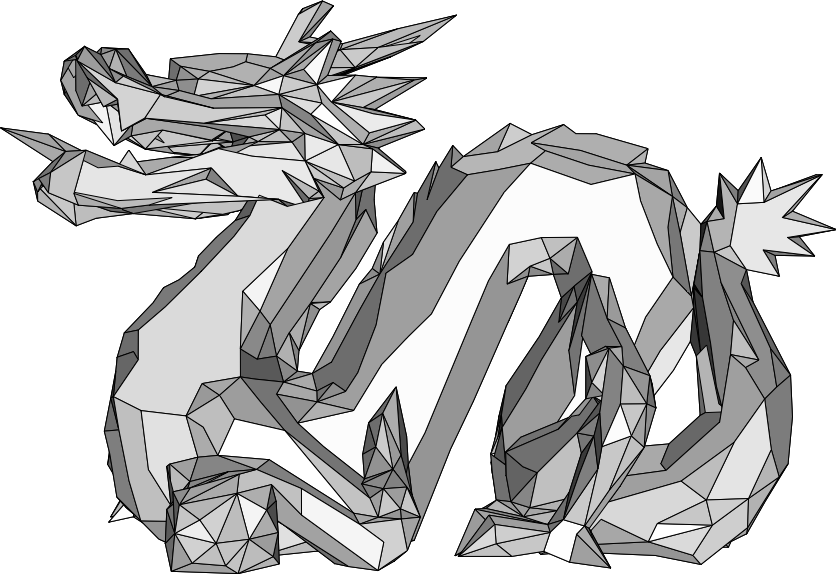
Originalmodell eines chinesischen Drachens mit 2730 Facetten.
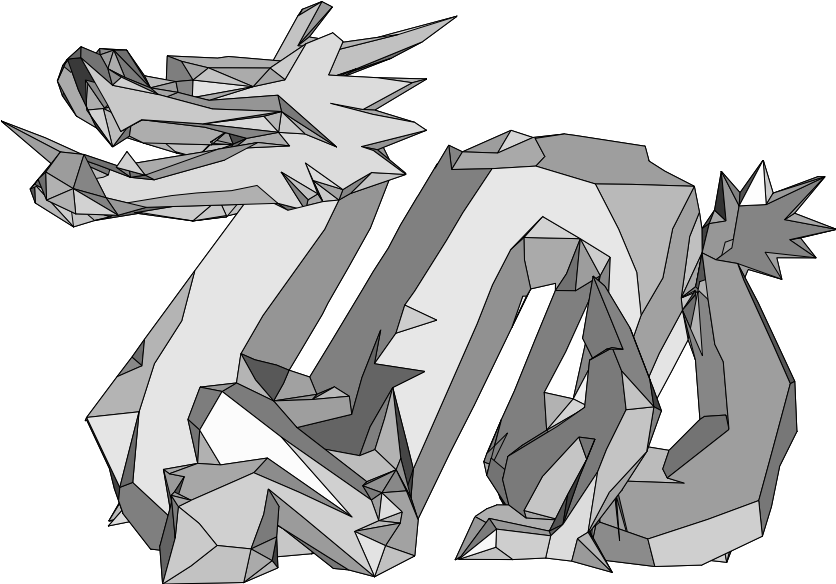Mit dem Netzreduktionsalsgorithmus auf 2268 Facetten vereinfachtes Modell. Halber Öffnungswinkel α=5°, keine Optimierung.	Mit dem Netzreduktionsalsgorithmus auf 1531 Facetten vereinfachtes Modell. Halber Öffnungswinkel α=10°, keine Optimierung.	Mit dem Netzreduktionsalsgorithmus auf 1045 Facetten vereinfachtes Modell. Halber Öffnungswinkel α=15°, keine Optimierung.