Übersicht
Details
In dieser Studienarbeit wurde Kobbelts (interpolierender) Umbrella-Algorithmus mittels verschiedener Variationsmethoden abgewandelt, und anschließend die Flächengüte mit Hilfe diskreter Krümmungsmaße berechnet. Der Umbrella-Algorithmus arbeitet grob wie folgt: Zu Anfang wird in der Mitte jeder Kante eines Dreiecksnetzes ein neuer Knoten erzeugt und diese Knoten dann verbunden. Unter Einhaltung der Interpolationsbedingung, daß bereits bestehende Knoten nicht wieder bewegt werden, wird anschließend die diskrete mittlere Krümmung des Netzes (global) minimiert, indem ein dünn besetztes Gleichungssystem gelöst wird.
Um genauere Vergleichsmöglichkeiten zu haben, werden zunächst NURBS-Flächen und beliebige, zugehörige Flächenkurven erzeugt. Diese Kurven dienen, nun unabhängig von ihrer Trägerfläche, als Ausgangspunkt der Flächeninterpolation. Schlußendlich bietet es sich auch an, zusätzlich den Abstand der Interpolationsfläche zur Ausgangsfläche zu berechnen um ein weiteres Gütekriterium für die verschiedenen Variationsmethoden und Interpolationsparameter miteinzubeziehen.
Anfangs werden die exakt vorliegenden Kurven äquidistant abgetastet, um eine erste Punktmenge zu erhalten. Diese wird dann mit dem Ball-Pivoting-Algorithmus oder gegebenenfalls mit einem 2D-Delaunay-Verfahren trianguliert.
 |
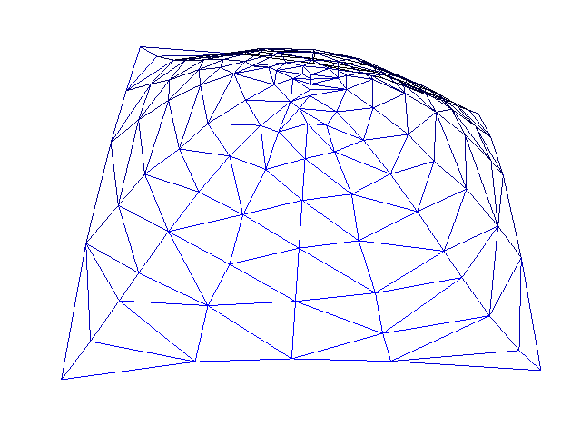 |
| Standard-NURBS-Fläche mit acht Flächenkurven (links). Nach Abtastung berechnet der Ball-Pivoting-Algorithmus eine Triangulierung aus der Kurvenpunktmenge (rechts). |
|
 |
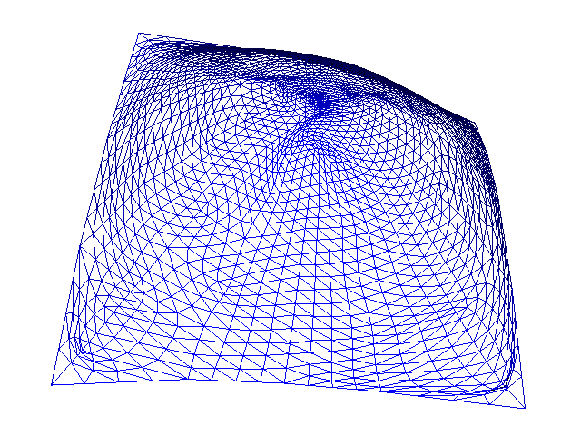 |
| Erster (links) und zweiter (rechts) Interpolationsschritt des Umbrella-Algorithmus mit unten beschriebenen Variationsarten. |
|
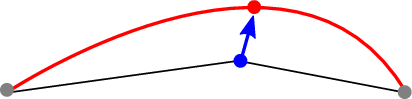
Weil die Interpolationsfläche nur vom zu Beginn erhaltenen Punkten abhängt, werden, als erster Modifikationsschritt, die bei der Unterteilung generierten Zwischenpunkte in Richtung der Kurve verschoben (Mittelpunktsvariation). Die Kurve ist im folgenden schematischen Bild rot dargestellt, während der Zwischenpunkt blau markiert ist.
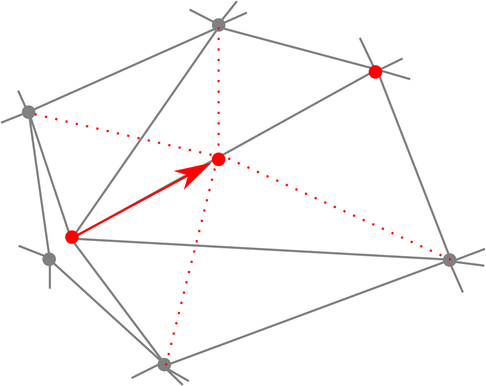
Eine andere Variationsart versucht, bei der Unterteilung degenerierenden Dreiecksfächer entgegenzuwirken, indem der mittlere Punkt modifiziert wird. (Fächervariation)
Ergebnisse
Die Interpolationsflächen besitzen nach Anwendung der unterschiedlichen Variationsschemata größtenteils kleinere mittlere Krümmung als vorher. Auch der (Hausdorff-)Abstand zu den Ausgangsflächen verminderte sich sowohl durch weitere Unterteilungsschritte als auch beispielsweise durch die Fächervariation. Verbesserungsmöglichkeiten ergeben sich etwa durch Wahl eines geeigneteren Triangulierungsalgorithmus oder weitere Variationsschemata.
